物理の問題を解く際、グラフを正しく読み取り、描くことは非常に重要です。特に自由落下のような運動では、グラフから多くの情報を読み取ることができます。
本記事では、自由落下のグラフについて詳しく解説し、v-tグラフ(速度-時間グラフ)やx-tグラフ(変位-時間グラフ)の特徴を説明していきます。グラフが原点を通る場合と通らない場合の違いや、グラフの傾きや面積が持つ物理的意味についても理解を深めましょう。
それでは、自由落下のグラフについて順を追って見ていきましょう。
自由落下のv-tグラフ(速度-時間グラフ)
それではまず自由落下のv-tグラフについて解説していきます。
v-tグラフの基本的な形
自由落下のv-tグラフは、原点を通る直線となります。これは速度vが時間tに比例するためです。自由落下の速度は v = gt という式で表されるため、グラフは傾きgの直線になるのです。
横軸に時間t、縦軸に速度vをとると、グラフは右上がりの直線となります。時間が経過するほど速度が増加していくことを視覚的に理解できるでしょう。
重力加速度gを10m/s²とした場合、1秒後に10m/s、2秒後に20m/s、3秒後に30m/sというように、等間隔で速度が増加していきます。
v-tグラフの傾きの意味
v-tグラフの傾きは加速度を表します。自由落下では加速度が常に重力加速度gで一定であるため、グラフの傾きも一定となるのです。
傾き = Δv/Δt = (v₂ – v₁)/(t₂ – t₁) = g となります。例えば、1秒から2秒の間に速度が10m/sから20m/sに変化した場合、傾きは (20-10)/(2-1) = 10 m/s² となるでしょう。
【v-tグラフの傾きと加速度】
傾き = 加速度
自由落下の場合:傾き = g ≒ 9.8 m/s²
グラフが直線 → 加速度が一定(等加速度運動)
v-tグラフの面積の意味
v-tグラフと時間軸で囲まれた部分の面積は、変位(移動距離)を表します。これは積分の概念に基づいており、速度を時間で積分すると変位が得られるという関係を反映しています。
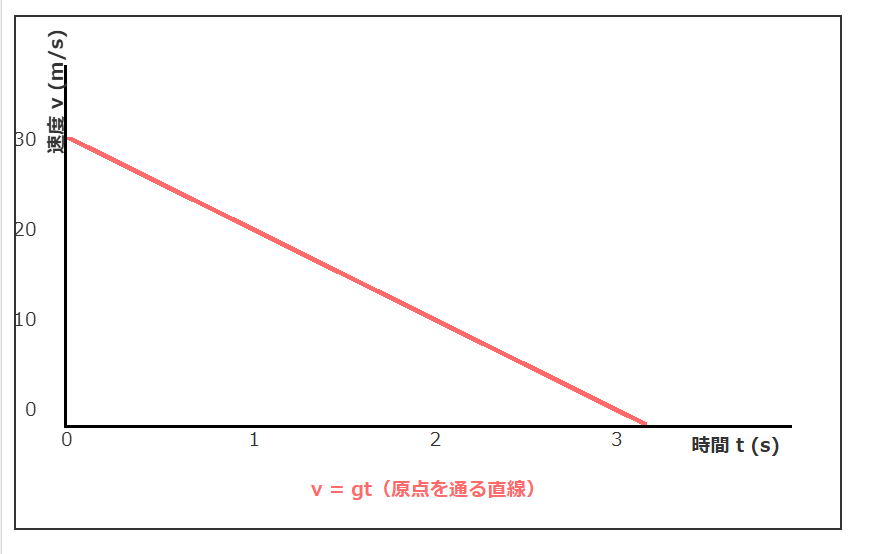
自由落下のv-tグラフは直線なので、囲まれる図形は三角形となります。三角形の面積 = (1/2) × 底辺 × 高さ = (1/2) × t × (gt) = (1/2)gt² となり、これは自由落下の変位の公式と一致するでしょう。
自由落下のx-tグラフ(変位-時間グラフ)
続いては自由落下のx-tグラフを確認していきます。
x-tグラフの基本的な形
自由落下のx-tグラフは、原点を通る放物線(下に凸の曲線)となります。変位xは時間tの2乗に比例するため、x = (1/2)gt² というグラフになるのです。
このグラフは時間が経つにつれて傾きが急になっていきます。これは時間が経過するほど速度が大きくなり、単位時間あたりの移動距離が増えるためです。
例えば、g = 10m/s²の場合、1秒後に5m、2秒後に20m、3秒後に45mと、時間の2乗に比例して落下距離が増加するでしょう。
x-tグラフの傾きの意味
x-tグラフの傾きは速度を表します。放物線のグラフでは、時間が経つにつれて傾きが大きくなることがわかります。これは速度が増加していることを示しているのです。
ある時刻における接線の傾きが、その瞬間の速度となります。数学的には、傾き = dx/dt = v であり、微分によって速度が求められるという関係です。
| 時刻(秒) | 変位(m) | 速度(m/s) | グラフの傾き |
|---|---|---|---|
| 0 | 0 | 0 | 0(水平) |
| 1 | 5 | 10 | 10 |
| 2 | 20 | 20 | 20 |
| 3 | 45 | 30 | 30 |
x-tグラフが原点を通る理由
自由落下のx-tグラフが原点を通るのは、時刻t = 0で変位x = 0という初期条件を設定しているためです。つまり、落下を開始した位置を原点(基準点)としているのです。
もし落下開始位置を地面から高さh₀の位置に設定した場合、グラフの式は x = h₀ – (1/2)gt² となり、原点を通らなくなります。この場合、グラフはy切片h₀を持つ放物線となるでしょう。
グラフが原点を通るかどうかは、座標系の取り方(どこを原点とするか)によって決まります。物理の本質は変わりませんが、グラフの見た目は変化するのです。
自由落下の加速度-時間グラフ
続いては自由落下の加速度-時間グラフを確認していきます。
a-tグラフの特徴
自由落下の加速度-時間グラフは、時間軸に平行な直線となります。これは加速度が常に一定値g(約9.8m/s²)であることを示しています。
このグラフは等加速度運動の特徴を視覚的に表しています。加速度が一定であることが、自由落下が等加速度直線運動である理由なのです。
a-tグラフの面積の意味
a-tグラフと時間軸で囲まれた面積は、速度の変化量を表します。面積 = a × t = g × t = Δv となり、これは速度の増加分に相当するでしょう。
例えば、0秒から3秒までの面積は 9.8 × 3 = 29.4 m/s となり、3秒間で速度が29.4m/s増加したことを意味します。初速度がゼロなので、3秒後の速度は29.4m/sとなるのです。
【a-tグラフから読み取れる情報】
・グラフの高さ:加速度の大きさ
・グラフの面積:速度の変化量
・水平な直線:等加速度運動
他の運動との比較
等加速度運動ではa-tグラフは水平線となりますが、加速度が変化する運動では異なる形になります。例えば、空気抵抗がある場合の落下運動では、加速度が時間とともに減少するため、グラフは下降曲線となるでしょう。
| 運動の種類 | a-tグラフの形 | 特徴 |
|---|---|---|
| 自由落下 | 水平な直線 | 加速度一定(g) |
| 等速直線運動 | a = 0の直線 | 加速度ゼロ |
| 空気抵抗あり落下 | 下降曲線 | 加速度減少 |
グラフから運動を読み解く方法
続いてはグラフから運動を読み解く方法を確認していきます。
3つのグラフの関係
x-tグラフ、v-tグラフ、a-tグラフは互いに密接な関係があります。微分と積分の関係で結ばれており、一つのグラフから他のグラフの情報を読み取ることができるのです。
x-tグラフの傾き → v-tグラフの値
v-tグラフの傾き → a-tグラフの値
v-tグラフの面積 → x-tグラフの変化量
a-tグラフの面積 → v-tグラフの変化量
これらの関係を理解することで、一つのグラフから運動の全体像を把握できるようになるでしょう。
グラフを使った問題の解き方
物理の問題では、グラフから数値を読み取ったり、グラフを描いたりする問題がよく出題されます。グラフ問題を解く際のポイントをまとめましょう。
【グラフ問題を解くコツ】
1. グラフの種類(v-t、x-t、a-t)を確認
2. 傾きが何を表すかを考える
3. 面積が何を表すかを考える
4. 原点を通るか、切片があるかを確認
5. グラフの形(直線、曲線)から運動の種類を判断
例えば、v-tグラフが原点を通る直線なら自由落下、切片がある直線なら初速度を持つ運動、曲線なら加速度が変化する運動と判断できます。
実際の問題への応用
グラフを使えば、複雑な計算をせずに運動の様子を理解できる場合があります。視覚的に運動を捉えることで、直感的な理解が深まるのです。
例えば、2つの物体の運動を比較する問題では、両方のv-tグラフを同じ座標系に描くことで、どちらが速いか、いつ追い越すかなどを一目で判断できるでしょう。
また、グラフの面積を利用することで、積分計算をせずに変位や速度変化を求められます。特に台形や三角形の面積公式を使えば、簡単に計算できる場合が多いのです。
まとめ
自由落下のグラフには3つの基本形があります。v-tグラフは原点を通る直線で傾きが加速度g、面積が変位を表します。x-tグラフは原点を通る放物線で傾きが速度を表し、時間の2乗に比例して変位が増加します。a-tグラフは高さgの水平線で、面積が速度変化を表すのです。
これらのグラフは微分と積分の関係で結ばれており、一つのグラフから他のグラフの情報を読み取ることができます。グラフの傾きや面積が持つ物理的意味を理解することで、運動を視覚的に捉え、問題を効率的に解くことができるようになるでしょう。
グラフが原点を通るかどうかは座標系の取り方によって変わりますが、物理の本質は変わりません。グラフを正しく読み解く力は、物理学習において非常に重要なスキルとなります。