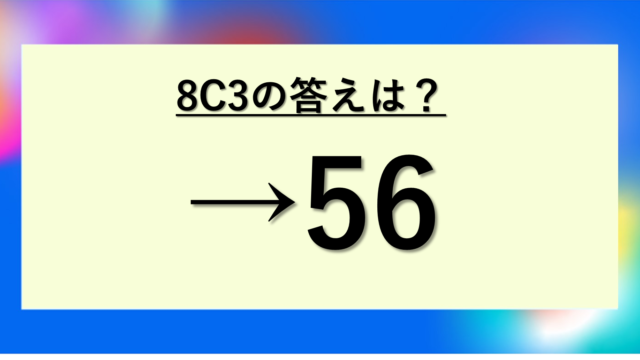
五角形の外角の和は？内角の和との関係も解説！（360度：多角形の外角：公式：性質：定理など

五角形の外角の和は何度になるでしょうか。

多角形を学ぶ際、内角の和については詳しく習いますが、外角の和についてはやや馴染みが薄いかもしれません。

実は、五角形の外角の和は360度です。

この値は五角形だけでなく、すべての多角形に共通する非常に重要な性質なのです。

外角とは、多角形の各頂点において、1つの辺を延長したときにできる角のこと。

内角とは隣り合う関係にあり、互いに補角を成しています。

五角形の内角の和が540度であることと比較すると、外角の和が360度であることには興味深い対称性があるでしょう。

本記事では、五角形の外角の和がなぜ360度になるのか、その求め方と証明方法を詳しく解説していきます。

内角の和との関係性や、n角形全般に適用できる外角の定理についても確認しましょう。

多角形の外角に関する理解を深めることで、図形問題への応用力が高まります。

五角形の外角の和は360度

それではまず、五角形の外角の和について基本的な内容を解説していきます。

五角形に限らず、すべての多角形の外角の和は360度という驚くべき性質があります。

三角形でも四角形でも六角形でも、辺の数に関わらず外角の和は常に一定なのです。

外角とは何か

外角の定義を正しく理解することが重要でしょう。

多角形の各頂点において、隣り合う2つの辺のうち1つを延長すると、もう1つの辺との間に角ができます。

これが外角です。

内角と外角は直線上に並んでいるため、内角+外角=180度という関係が成り立ちます。

五角形には5つの頂点がありますから、外角も5つ存在します。

各頂点で内角と外角が補角の関係にあることを覚えておきましょう。

なぜ360度になるのか

五角形の外角の和が360度になる理由を直感的に理解する方法があります。

多角形の周りを1周すると考えてみましょう。

ある頂点から出発して、各辺に沿って進み、すべての頂点を通って元の位置に戻ってきます。

このとき、各頂点で曲がる角度の合計が外角の和に相当するのです。

1周すると向きが元に戻りますから、合計の回転角は360度になります。

この考え方は、五角形だけでなくすべての凸多角形に当てはまる普遍的な原理です。

内角の和との違い

五角形の内角の和は540度ですが、外角の和は360度。

この違いはどこから生まれるのでしょうか。

内角の和は、多角形の辺の数が増えるほど大きくなります。

三角形は180度、四角形は360度、五角形は540度と、辺が1つ増えるごとに180度ずつ増加していくのです。

一方、外角の和は辺の数に関わらず常に360度で一定。

この対照的な性質が、多角形の幾何学的な美しさを示しているでしょう。

多角形	辺の数	内角の和	外角の和
三角形	3	180度	360度
四角形	4	360度	360度
五角形	5	540度	360度
六角形	6	720度	360度
八角形	8	1080度	360度

五角形の外角の和の求め方と証明

続いては、五角形の外角の和を実際に求める方法と証明を確認していきます。

外角の和を求める方法には、いくつかのアプローチがあります。

最も基本的なのは、内角との関係を利用する方法でしょう。

内角を利用した求め方

五角形の各頂点において、内角と外角は補角の関係にあります。

つまり、内角+外角=180度です。

五角形には5つの頂点がありますから、この式を5つの頂点すべてについて足し合わせてみましょう。

このように、内角の和を知っていれば外角の和も簡単に求められます。

五角形の内角の和540度という値が、外角の和を導く鍵になっているのです。

一般公式による証明

n角形全般について、外角の和が360度であることを証明してみましょう。

n角形にはn個の頂点があり、各頂点で内角と外角の和は180度です。

すべての頂点について足し合わせると、(内角の和)+(外角の和)=180度×nとなります。

n角形の内角の和は180度×(n−2)ですから、これを代入すると次のようになるでしょう。

この証明から分かるように、nの値に関わらず外角の和は常に360度になります。

三角形でも十角形でも、辺の数によらず同じ結果が得られるのです。

回転による直感的理解

外角の和が360度であることは、図形の回転という観点からも理解できます。

多角形の辺に沿って進む人を想像してみてください。

各頂点に到着するたびに、次の辺の方向へ向きを変えます。

この向きの変化の角度が、まさに外角に相当するのです。

多角形を1周して出発点に戻ってくると、向きも元通りになっています。

つまり、合計で1回転(360度)したことになるわけです。

五角形なら5回曲がって1周、六角形なら6回曲がって1周しますが、どちらも合計の回転角は360度。

この直感的なイメージが、外角の和の定理を理解する助けになるでしょう。

五角形の内角の和と外角の和の関係

続いては、五角形における内角の和と外角の和の関係性を確認していきます。

内角と外角は密接に関連しており、一方が分かればもう一方も求められます。

この関係性を理解することで、図形問題への応用範囲が広がるでしょう。

補角の関係から導かれる性質

各頂点において内角と外角は補角ですから、内角+外角=180度が成り立ちます。

五角形の5つの頂点すべてでこの関係があるため、(内角の和)+(外角の和)=180度×5=900度となるのです。

内角の和が540度なら外角の和は360度、外角の和が360度なら内角の和は540度。

このように、内角の和と外角の和を足すと常に180度×辺の数になります。

正五角形における具体例

正五角形では、すべての内角が等しく、すべての外角も等しくなります。

内角の和が540度ですから、1つの内角は540度÷5=108度。

外角の和が360度ですから、1つの外角は360度÷5=72度です。

実際に、108度+72度=180度となり、補角の関係が確認できるでしょう。

正多角形の場合、1つの外角を求める公式は360度÷辺の数となります。

正六角形なら360度÷6=60度、正八角形なら360度÷8=45度という具合です。

正多角形	1つの内角	1つの外角	内角+外角
正三角形	60度	120度	180度
正四角形	90度	90度	180度
正五角形	108度	72度	180度
正六角形	120度	60度	180度
正八角形	135度	45度	180度

不規則な五角形での応用

不規則な五角形でも、内角の和と外角の和の関係は変わりません。

たとえば、ある五角形の4つの外角が80度、60度、75度、70度だとしましょう。

外角の和は360度ですから、残りの外角は360度−(80+60+75+70)=75度と求められます。

また、この五角形の内角を求めたい場合、各外角から180度を引けば良いのです。

このように、内角と外角の関係を理解していれば、片方から もう片方を自由に求められます。

多角形の外角の和の性質と定理

続いては、五角形を含む多角形全般の外角の和について確認していきます。

外角の和が360度という性質は、多角形の幾何学において非常に重要な定理です。

この性質を様々な角度から理解することで、図形問題への応用力が身につくでしょう。

凸多角形と凹多角形

外角の和が360度という定理は、凸多角形に限らず凹多角形にも適用されます。

凸多角形とは、すべての内角が180度未満の多角形のこと。

一方、凹多角形は1つ以上の内角が180度を超える多角形です。

凹多角形では、一部の外角が負の値(内側に向かう角)として扱われることがありますが、符号を考慮して計算すると外角の和はやはり360度になります。

ただし、一般的な学習段階では凸多角形を対象とすることが多いでしょう。

外角の和を使った問題

外角の和が360度であることを利用すると、様々な問題が解けます。

例えば、「正n角形の1つの外角が40度のとき、nの値を求めよ」という問題を考えてみましょう。

正n角形では、すべての外角が等しいため、1つの外角×n=360度が成り立ちます。

また、「ある多角形の外角の和は何度か」という問題に対しては、辺の数に関わらず常に360度と答えられます。

これは外角の和の定理を知っていれば即答できる問題です。

実生活での応用例

外角の和の性質は、実際の場面でも応用されています。

例えば、道路設計において曲がり角の角度を決める際、一周して元の方向に戻るようなコースを作るには、すべての曲がり角(外角)の合計が360度になるように設計します。

また、ロボットの移動経路をプログラミングする際も、多角形の経路を一周させるには外角の合計を360度にする必要があるのです。

建築やデザインの分野でも、多角形の外角の性質を理解していることで、より効率的な設計が可能になるでしょう。

さらに、測量の分野では、土地の境界を測定する際に外角の和が360度になることを利用して、測定誤差をチェックすることもあります。

まとめ

五角形の外角の和は360度であり、これはすべての多角形に共通する普遍的な性質です。

各頂点において内角と外角は補角の関係にあり、内角+外角=180度が成り立ちます。

五角形の5つの頂点すべてでこの関係を足し合わせると、(内角の和)+(外角の和)=900度となり、内角の和が540度であることから外角の和は360度と求められるのです。

外角の和が360度になる理由は、多角形の周りを1周したときの回転角が360度であることとも対応しています。

正五角形の場合、1つの外角は360度÷5=72度となり、内角の108度と足すと180度になることが確認できるでしょう。

この性質は、n角形全般に適用できる重要な定理であり、三角形でも六角形でも外角の和は常に360度です。

内角の和は辺の数によって変化しますが、外角の和は常に一定という対照的な性質が、多角形の幾何学的な美しさを示しています。

外角の和の理解は、図形問題を解く上での基礎となり、測量や設計など実生活でも応用される重要な知識です。