鉛直方向と水平方向の違いは？運動の公式は？（物理：座標軸：等加速度運動：水平投射・斜方投射など）

物理の運動を学ぶ上で、鉛直方向と水平方向の違いを正確に理解することは極めて重要です。特に投射運動を扱う際、この2つの方向で運動の性質が大きく異なることを知っておく必要がありますね。

鉛直方向と水平方向の最も本質的な違いは、重力が働くかどうかという点にあります。鉛直方向には常に重力加速度gが働くため等加速度運動になり、水平方向には重力が働かないため等速直線運動になるのです。

この違いを理解することで、水平投射や斜方投射といった2次元の運動を、独立した2つの1次元運動の組み合わせとして扱えるようになります。それぞれの方向で適切な運動方程式を立て、座標軸を設定して解くことが、問題解決の鍵となるでしょう。

本記事では、鉛直方向と水平方向の違いから、それぞれに適用される運動の公式、座標軸の設定方法、そして水平投射や斜方投射への応用まで、体系的に解説していきます。運動を方向ごとに分解して考える技術を身につけることで、複雑な物理問題もすっきりと理解できるようになるはずです。

鉛直方向は等加速度運動で水平方向は等速直線運動になる

それではまず、鉛直方向と水平方向における運動の本質的な違いについて解説していきます。

鉛直方向と水平方向を理解する出発点は、重力の影響です。地球上の物体には常に重力が働いており、この重力は鉛直下向きにのみ作用します。これが2つの方向で運動の性質を決定的に変えるのです。

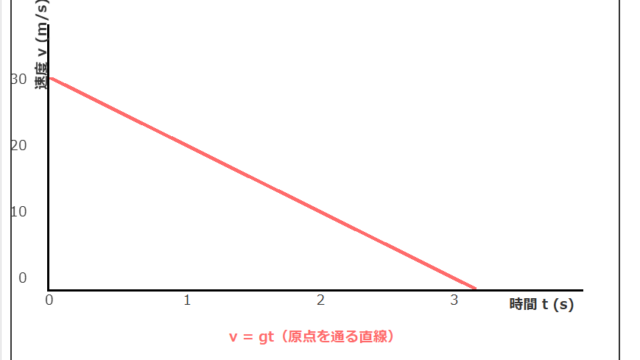
鉛直方向では、重力加速度gによって物体は常に下向きに加速されます。上向きに運動している場合は減速し、下向きに運動している場合は加速するわけですね。一方、水平方向には力が働かないため、一度与えられた速度は変化せず、等速直線運動を続けるのです。

この性質の違いにより、2次元の運動を扱う際は、鉛直成分と水平成分を独立に扱えるという重要な原理が生まれます。それぞれの方向で異なる運動方程式を使い、最後に結果を合成すればよいのです。

項目	鉛直方向	水平方向
重力の影響	あり（下向きにg）	なし
加速度	−g または +g（座標系による）	0
運動の種類	等加速度運動	等速直線運動
速度の変化	時間とともに変化	一定
使う公式	v = v₀ ± gt、y = v₀t ± (1/2)gt²	v = v₀、x = v₀t

空気抵抗を無視できる場合、水平方向の運動は非常にシンプルになります。初速度v₀xを持っていれば、その速度のまま進み続けるだけですね。一方、鉛直方向は重力の影響を常に受けるため、時々刻々と速度が変化していくのです。

この違いを理解していれば、例えば「物体を水平に投げた場合、どこまで飛ぶか」という問題も、水平方向の等速運動と鉛直方向の等加速度運動を組み合わせることで解けるようになります。それぞれの方向で独立に時間の関数として位置を求め、最後に合成すればよいわけです。

鉛直方向と水平方向の運動方程式と公式

続いては、それぞれの方向で使用する具体的な運動方程式と公式を確認していきます。

鉛直方向の運動方程式と3つの基本公式

鉛直方向の運動は等加速度運動であり、加速度が−g（上向きを正とする場合）または+g（下向きを正とする場合）となります。使用する公式は等加速度運動の一般式から導かれますね。

これらの公式において、符号に注意することが極めて重要です。上向きを正の方向とする座標系では、重力は負の加速度−gとして現れます。逆に下向きを正とすれば、+gになるわけですね。

鉛直方向の運動では、時間とともに速度が変化します。上向きに投げられた物体は徐々に減速し、最高点で速度が0になり、その後は下向きに加速していくのです。この速度の変化を記述するのが鉛直方向の公式でしょう。

水平方向の運動方程式と等速運動の公式

水平方向の運動は、加速度が0の等速直線運動です。したがって、使用する公式は非常にシンプルになりますね。

水平方向では、初速度v₀xがそのまま保たれ続けます。加速度が0なので、速度は時間が経っても変化しないのです。変位は単純に「速度×時間」で求められますね。

この単純さが、水平方向の計算を容易にします。例えば、物体が空中にいる時間（滞空時間）が分かれば、水平到達距離は v₀x × t で即座に計算できるわけです。滞空時間は鉛直方向の運動から決まるため、鉛直方向で時間を求め、水平方向で距離を求めるという手順になります。

座標軸の設定方法と符号の扱い方

鉛直方向と水平方向を扱う際、座標軸を適切に設定することが問題を正しく解く鍵となります。座標系の設定によって、公式の符号が変わるためですね。

上向きを正とする座標系が最も一般的です。この場合、重力は下向きに働くため−gとなります。もし下向きを正とする座標系を選ぶなら、重力は+gになり、公式の符号も変わるわけですね。

重要なのは、一度設定した座標系を問題全体を通して一貫して使うことです。途中で座標系を変えると、符号の混乱が生じて計算ミスにつながります。問題を解き始める前に、まず座標軸を明確に設定し、図に書き込んでおくとよいでしょう。

座標系の選び方に絶対的なルールはありませんが、上向きを正とする方が多くの教科書や参考書と一致するため、混乱が少ないでしょう。ただし、問題によっては下向きを正とした方が計算しやすい場合もあるため、状況に応じて適切に選択することが重要です。

水平投射における鉛直方向と水平方向の運動

続いては、水平投射を例に、2つの方向の運動がどのように組み合わさるかを確認していきます。

水平投射の定義と運動の特徴

水平投射とは、物体を水平方向に初速度v₀を与えて投げ出す運動のことです。鉛直方向の初速度は0であり、重力の影響だけで落下していきますね。

水平投射の特徴は次のようにまとめられます。

水平投射では、物体は放物線を描いて飛んでいきます。この放物線は、水平方向の等速運動と鉛直方向の等加速度運動が組み合わさった結果として現れるのです。

水平投射の運動を理解するポイントは、2つの方向の運動が互いに独立していることでしょう。水平方向の速度は鉛直方向の運動に影響されず、鉛直方向の落下運動も水平方向の速度に影響されません。

水平投射の到達距離と落下時間の計算

水平投射の典型問題として、到達距離（水平到達距離）を求める問題があります。これは鉛直方向と水平方向の運動を組み合わせて解きますね。

この解法の手順が典型的なパターンです。まず鉛直方向の運動から時間を求め、その時間を使って水平方向の変位を計算するわけですね。2つの方向を別々に扱うことで、複雑な2次元運動が単純な1次元運動の組み合わせになります。

落下時間は高さhにのみ依存し、水平方向の初速度には依存しません。どんなに速く投げても、ゆっくり投げても、同じ高さから落とせば落下時間は同じなのです。これが、2方向の運動が独立していることの証明になりますね。

水平投射における速度ベクトルの変化

水平投射では、時間とともに速度ベクトルの向きと大きさが変化していきます。これも2方向の運動を合成することで理解できるでしょう。

投げ出した直後は、速度はほぼ水平ですが、時間が経つにつれて鉛直下向きの成分が大きくなり、速度ベクトルは徐々に下向きに傾いていきます。地面に達する直前には、かなり急な角度で落下することになるわけですね。

速度の大きさも時間とともに増加します。水平成分は一定ですが、鉛直成分が増え続けるため、合成速度の大きさは単調増加するのです。これは物体が落下しながら加速していることを意味しますね。

斜方投射における2方向の運動の分解と合成

続いては、より一般的な斜方投射について、2方向の運動がどのように扱われるかを確認していきます。

斜方投射の初速度を2方向に分解する方法

斜方投射とは、水平方向に対して角度θで物体を投げ出す運動のことです。初速度v₀が斜め方向を向いているため、まずこれを水平成分と鉛直成分に分解する必要がありますね。

初速度の分解には三角関数を使います。角度θが水平方向から測った仰角である場合、水平成分はcos θ、鉛直成分はsin θを使うわけですね。この分解さえできれば、後は水平方向と鉛直方向でそれぞれの公式を適用するだけです。

45度の場合、水平成分と鉛直成分は等しくなります。これは、45度が最も水平到達距離が大きくなる角度であることと関係していますね。角度が45度より小さいと鉛直成分が減り滞空時間が短くなり、45度より大きいと水平成分が減って水平速度が遅くなるのです。

斜方投射の最高点と到達距離の求め方

斜方投射では、最高点の高さと水平到達距離が主要な求めるべき量になります。これらも2方向の運動を組み合わせて求めますね。

最高点の高さは鉛直方向の運動だけから決まります。鉛直方向の初速度v₀y = v₀ sin θを使って、v² − v₀² = −2gy に v = 0 を代入すれば求められるわけですね。

水平到達距離は、全滞空時間と水平方向の速度の積として求められます。滞空時間は鉛直方向の運動から、水平速度は初速度の水平成分から、それぞれ独立に求めるのです。

斜方投射における軌道の方程式

斜方投射の軌道は放物線になりますが、この軌道の方程式も2方向の運動方程式から導けます。時間tを消去することで、y を x の関数として表すのです。

この方程式は、xの2次関数になっており、放物線を表していますね。係数を見ると、v₀yが大きいほど高く上がり、v₀xが大きいほど遠くまで飛ぶことが分かります。

軌道方程式を使えば、任意の水平位置xでの高さyを直接計算できます。これは、物体がある障害物を越えられるかどうかを判定する問題などで役立つでしょう。

実践問題で理解を深める鉛直方向と水平方向の扱い

続いては、具体的な問題を通して、2方向の運動の扱い方を確認していきます。

高台からの水平投射の応用問題

高台からの投射では、初期位置が地面より高いという条件が加わります。座標系の原点設定が重要になる問題ですね。

この問題では、鉛直方向で時間を求め、その時間での水平変位と速度成分を求め、最後に速度ベクトルの大きさを計算しています。各ステップで適切な方向の公式を使うことがポイントでしょう。

斜方投射で特定の高さを通過する問題

斜方投射で、ある高さを通過する時刻や水平位置を求める問題も重要です。これも2方向の運動を組み合わせて解きますね。

この問題では、判別式が0になり解が1つだけ得られました。これは高さ15mが最高点の高さと一致していることを意味します。通常、ある高さを通過する時刻は2つ（上昇中と下降中）ありますが、最高点では1つになるわけですね。

2つの物体の運動を比較する問題

異なる条件で投射された2つの物体を比較する問題では、それぞれの方向での運動を整理することが重要でしょう。

この結果から、30度と60度は補角の関係にあり、水平到達距離が等しくなることが分かりますね。一方、最高点の高さは角度が大きいほど高くなります。このように、鉛直成分と水平成分を分けて考えることで、様々な条件を比較できるのです。

まとめ

鉛直方向と水平方向の最も本質的な違いは、重力が働くかどうかという点にあります。鉛直方向には重力加速度gが常に働くため等加速度運動になり、水平方向には力が働かないため等速直線運動になるのです。

それぞれの方向で使用する公式も異なります。鉛直方向では v = v₀ ± gt、y = v₀t ± (1/2)gt² などの等加速度運動の公式を使い、水平方向では v = v₀、x = v₀t という等速運動の公式を使いますね。座標軸を適切に設定し、符号に注意することが正確な計算の鍵となるでしょう。

水平投射や斜方投射といった2次元の運動は、鉛直方向と水平方向の運動が独立に起こり、それらが合成されたものとして理解できます。鉛直方向で時間や高さを求め、水平方向で距離を求めるという手順で、複雑な問題も体系的に解けるのです。

斜方投射では、初速度をまず水平成分と鉛直成分に分解することから始めます。三角関数を使った分解さえできれば、後はそれぞれの方向で独立に公式を適用すればよいわけですね。最高点の高さは鉛直成分だけから、水平到達距離は両方の成分から決まります。

2方向の運動を独立に扱えるという性質は、物理学における重要な原理です。この考え方は、より複雑な運動や力の分解にも応用されます。鉛直方向と水平方向の違いを正確に理解し、それぞれに適切な公式を使いこなせるようになることで、力学の問題に自信を持って取り組めるようになるでしょう。