数学の組み合わせの計算では、「7C3」のような記号を見かけることがよくあります。しかし、この記号が何を意味しているのか、どうやって計算すればいいのか、わからない方も多いのではないでしょうか。
7C3は「7個のものから3個を選ぶ組み合わせの数」を表す記号です。この記事では、7C3の具体的な計算方法や答え、さらには覚え方のコツまで詳しく解説していきます。
また、「7C3と7C4の答えが同じになる」という不思議な性質についても触れていきます。一見すると不思議に思えるこの関係には、組み合わせの本質的な意味が隠れているんです。
確率や場合の数の問題を解く上で、組み合わせの計算は避けて通れません。この記事を読めば、7C3の計算が自信を持ってできるようになるでしょう。それでは、順を追って見ていきましょう。
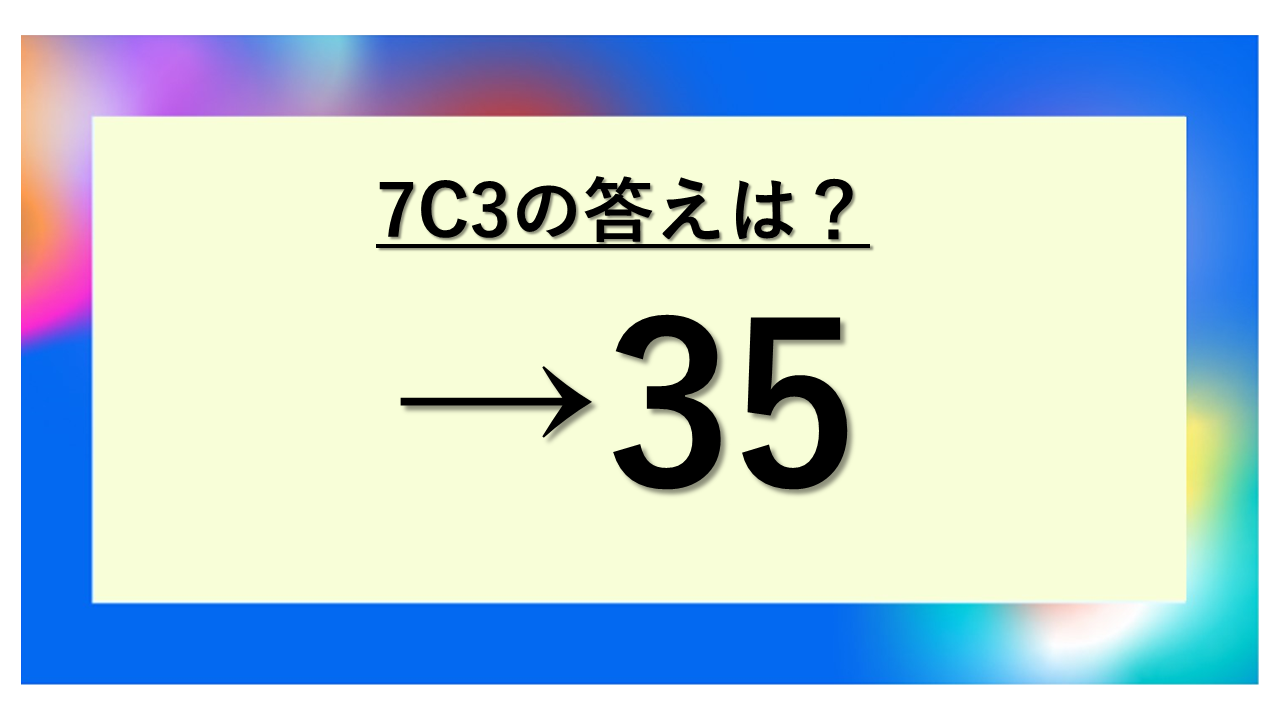
7C3の計算結果は35(組み合わせの答え)
それではまず、7C3の計算結果について解説していきます。
7C3の答えは35です。つまり、7個のものから3個を選ぶ組み合わせは35通りあります。
この数字は組み合わせの公式を使って計算することで求められます。7C3という記号は「Combination(コンビネーション)」の頭文字Cを使った表記で、数学では標準的な書き方なんです。
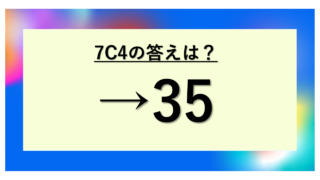
ちなみに、7C4も同じく35になります。これは偶然ではなく、組み合わせの性質によるもの。後ほど詳しく説明しますが、「選ぶもの」と「選ばないもの」が表裏一体の関係にあるためです。
組み合わせ(combination)とは何か
組み合わせとは、いくつかのものの中から、順番を考えずにいくつかを選び出す場合の数を指します。
例えば、A、B、C、D、E、F、Gという7人の中から3人を選ぶ場合を考えてみましょう。この時、「AさんとBさんとCさん」を選ぶのと「CさんとBさんとAさん」を選ぶのは同じ組み合わせとして扱われます。
順番が関係ないというのが組み合わせの大きな特徴です。これに対して、順番まで考慮する場合は「順列(permutation)」と呼ばれ、記号はPを使います。
日常生活でも組み合わせは頻繁に使われています。例えば、くじ引きで当選者を選ぶ、チームのメンバーを選ぶ、メニューから料理を選ぶなど、順番を気にしない選び方はすべて組み合わせなんです。
7C3が表す意味を具体例で理解する
7C3を具体的にイメージしてみましょう。
例えば、7種類のフルーツ(りんご、みかん、バナナ、ぶどう、いちご、メロン、桃)があり、その中から3種類を選んでフルーツパフェを作る場合を考えます。このとき、選べる組み合わせは全部で35通りになります。
別の例を挙げると、7人のクラスメイトから3人の委員を選ぶ場合も7C3です。誰が1番目に選ばれたかは関係なく、最終的に選ばれた3人が誰なのかだけが重要になります。
| 状況 | 7C3の適用例 |
|---|---|
| トランプ | 7枚のカードから3枚を選ぶ |
| スポーツ | 7人の選手から3人のスターティングメンバーを選ぶ |
| 旅行 | 7つの観光地から3つを訪れる |
| 食事 | 7つのおかずから3つを選ぶ |
このように、身近な場面でも7C3の考え方は活用されているんです。
組み合わせと順列の違いを押さえる
組み合わせを理解する上で、順列との違いを押さえておくことが重要でしょう。
組み合わせは順番を考えない、順列は順番を考えるというのが最大の違いです。
例えば、A、B、Cという3人から2人を選ぶ場合を考えてみます。組み合わせ(3C2)では、AB、AC、BCの3通りです。しかし順列(3P2)では、AB、BA、AC、CA、BC、CBの6通りになります。
つまり、同じ「選ぶ」という行為でも、順番が関係するかどうかで場合の数が大きく変わってくるんです。一般的に、順列の方が組み合わせよりも場合の数が多くなります。
問題を解く際には、「順番が関係あるのか、ないのか」をしっかり見極める必要があります。リレーの走順を決める場合は順列、委員を選ぶ場合は組み合わせといった具合ですね。
7C3の計算方法と公式の使い方
続いては7C3の具体的な計算方法を確認していきます。
組み合わせには決まった公式があり、それを使えば確実に答えを導き出せます。公式を暗記するだけでなく、その意味を理解することで応用力も身につくでしょう。
組み合わせの公式nCrとは
組み合わせの計算には、次の公式を使います。
nCr = n! / (r! × (n-r)!)
n:全体の個数、r:選ぶ個数
!(階乗):その数から1まで順に掛け合わせたもの
この公式において、「!」は階乗(かいじょう)と呼ばれる記号です。例えば、5! = 5×4×3×2×1 = 120 となります。
7C3の場合、n=7、r=3を公式に当てはめればいいわけです。階乗の概念は最初は難しく感じるかもしれませんが、慣れてしまえば機械的に計算できるようになります。
ちなみに、0! = 1 と定義されています。これは数学的な約束事として覚えておきましょう。
7C3を公式に当てはめて計算する手順
それでは実際に7C3を計算してみましょう。
7C3 = 7! / (3! × (7-3)!)
= 7! / (3! × 4!)
= (7×6×5×4×3×2×1) / ((3×2×1) × (4×3×2×1))
= (7×6×5×4!) / (3! × 4!)
= (7×6×5) / (3×2×1)
= 210 / 6
= 35
計算のポイントは、分子と分母に共通する階乗を約分することです。上の計算では4!を約分しています。
さらに詳しく見ると、分子の7×6×5は「7から3つの数を順に掛ける」、分母の3×2×1は「選ぶ個数の階乗」と覚えるとわかりやすいでしょう。
この方法を使えば、大きな階乗を全部計算しなくても答えが出せます。効率的な計算方法を身につけることが大切なんです。
計算を簡単にする工夫とテクニック
7C3の計算をさらに簡単にする方法があります。
実は、組み合わせの公式は次のように書き換えることもできるんです。
nCr = (n×(n-1)×(n-2)×…×(n-r+1)) / r!
7C3 = (7×6×5) / (3×2×1) = 210/6 = 35
この方法なら、分子は「7から始めて3個掛ける」、分母は「3の階乗」と覚えるだけで済みます。実際の計算でも、大きな階乗を全部展開する必要がないため、時間短縮になるでしょう。
また、nCr = nC(n-r)という性質を使うのも有効です。7C3を計算するより7C4を計算する方が楽な場合もありますが、この2つは等しいので、どちらを計算してもOKなんです。
電卓を使う場合は、最近の関数電卓にはnCrボタンが付いているものも多いです。ボタン一つで答えが出るので便利ですね。
7C3と7C4が同じ答えになる理由【なぜ】
続いては、7C3と7C4が同じ答えになる理由を確認していきます。
多くの人が「なぜ?」と疑問に思うこの性質には、組み合わせの本質が隠れています。
「選ぶ」と「選ばない」の対称性
7C3と7C4が等しくなる理由は、「3個を選ぶ」ことと「4個を選ばない」ことが同じだからです。
7個のものから3個を選ぶと、残りは4個になります。逆に言えば、7個から4個を選ぶと、残りは3個です。つまり、「どちらを選んだグループとして見るか」という視点の違いに過ぎないんです。
例えば、7人から3人の当選者を選ぶことは、7人から4人の落選者を選ぶことと表裏一体の関係にあります。当選者を決めれば自動的に落選者も決まりますし、その逆も成り立ちますよね。
この考え方は、組み合わせの計算を楽にするテクニックとしても使えます。計算が面倒な方を避けて、簡単な方を計算すればいいわけです。
公式で証明してみる
数式を使って7C3=7C4を証明してみましょう。
7C4 = 7! / (4! × 3!)
7C3 = 7! / (3! × 4!)
両者とも分子は7!、分母は3!×4!(順序が違うだけ)
よって 7C3 = 7C4
掛け算では順序を入れ替えても結果は同じなので、3!×4! = 4!×3! が成り立ちます。したがって、7C3と7C4は完全に一致するんです。
一般化すると、nCr = nC(n-r)という公式が成り立ちます。これは組み合わせの重要な性質の一つです。
この性質を知っていれば、例えば100C98を計算する際に、わざわざ98!を計算せず、100C2として計算できます。これは大きな時間短縮になるでしょう。
パスカルの三角形で視覚的に理解する
組み合わせの数を並べた「パスカルの三角形」を見ると、対称性がよくわかります。
| 1 | |||
| 1 | 1 | ||
| 1 | 2 | 1 | |
| 1 | 3 | 3 | 1 |
| … | 7C3=35 | … | 7C4=35 |
パスカルの三角形では、各行が左右対称になっています。7行目(n=7)を見ると、左から4番目と5番目の数字(それぞれ7C3と7C4)が等しくなっているんです。
この三角形は組み合わせの数を視覚的に表現したもので、数学の美しさを感じられる図形でもあります。眺めているだけで、組み合わせの性質が直感的に理解できるでしょう。
7C3の覚え方とコツ【確率・場合の数の勉強法】
続いては、7C3をはじめとする組み合わせの計算を効率よく習得するコツを確認していきます。
数学の勉強では、公式を丸暗記するだけでなく、その背景にある意味や使い方を理解することが重要です。
公式を覚えるための語呂合わせと記憶法
組み合わせの公式を覚えるには、いくつかのアプローチがあります。
まず、「nCrは、nから順にr個掛けて、r!で割る」と言葉で覚える方法があります。これなら公式の形を思い出しやすいでしょう。
また、「C」は「Choose(選ぶ)」の頭文字と覚えるのも効果的です。nCrは「n個からr個をChooseする」という意味だと理解できますね。
計算の際は、必ず約分できる部分を探すことがポイントになります。階乗の計算は数が大きくなりがちなので、早めに約分することで計算ミスを減らせるんです。
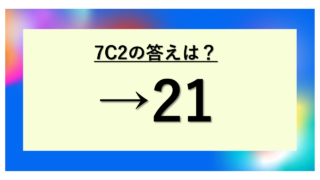
実際の試験では、7C3のような小さい数字は答えを覚えてしまうのも一つの手です。7C3=35、7C2=21、7C1=7といった頻出の値を覚えておくと、時間短縮になります。
練習問題で理解を深める方法
組み合わせの計算は、実際に手を動かして練習することが一番の近道です。
基本的な練習問題としては、次のようなものがおすすめでしょう。
練習1:5C2を計算してみましょう
答え:5×4/(2×1) = 10
練習2:8C3を計算してみましょう
答え:8×7×6/(3×2×1) = 56
練習3:10C7を計算してみましょう
答え:10C3と同じなので、10×9×8/(3×2×1) = 120
練習問題を解く際は、必ず途中式を書くことが大切です。暗算で済ませようとすると、計算ミスが増えてしまいます。
また、答えが合っているかどうかだけでなく、「なぜその公式を使うのか」「他の解き方はないか」と考えることで、理解が深まるでしょう。
組み合わせの問題は、確率の計算にも直結します。「全体の場合の数」や「特定の事象の場合の数」を求める際に、組み合わせの知識が必須になるんです。
応用問題への取り組み方
基本が身についたら、応用問題にも挑戦してみましょう。
例えば、「7人の中から少なくとも2人を選ぶ方法は何通りか」という問題では、7C2+7C3+7C4+7C5+7C6+7C7を計算する必要があります。
あるいは、「7個の異なるボールから3個を選び、さらにその3個に順番をつける方法は何通りか」という問題なら、7C3×3!という計算になります。組み合わせと順列を組み合わせた問題ですね。
応用問題では、問題文を正確に読み取り、何を求められているのかを明確にすることが重要です。「順番を考えるか考えないか」「全体から引き算するか足し算するか」といった判断が正答への鍵になります。
間違えた問題は、解答を見るだけでなく、「どこで間違えたのか」「どう考えれば正解できたのか」を分析することで、同じミスを繰り返さなくなるでしょう。
まとめ
7C3の計算方法と答えについて詳しく解説してきました。
7C3は「7個から3個を選ぶ組み合わせ」を表し、答えは35になります。計算には組み合わせの公式nCr = n!/(r!×(n-r)!)を使い、7C3 = 7×6×5/(3×2×1) = 35と求めることができるんです。
また、7C3と7C4が同じ答えになる理由は、「3個を選ぶ」ことと「4個を選ばない」ことが裏表の関係にあるためです。この性質nCr=nC(n-r)を理解しておくと、計算の効率が格段に上がるでしょう。
組み合わせの計算は、確率や場合の数の問題を解く上で欠かせないスキルです。公式を丸暗記するだけでなく、その意味を理解し、練習問題を繰り返すことで、自信を持って使えるようになります。
最初は難しく感じるかもしれませんが、一つ一つ丁寧に理解していけば、必ずマスターできます。7C3=35という答えとともに、その背景にある考え方もしっかり身につけていきましょう。