物理学において「変位」という概念は、位置の変化を表す重要な物理量です。自由落下を学ぶ際、変位と距離の違いを正しく理解することは、運動を正確に記述する上で欠かせません。
本記事では、自由落下における変位の意味と求め方を詳しく解説し、変位と距離の違いや、時間との関係について説明していきます。変位のグラフや具体的な計算方法まで幅広くご紹介しましょう。
それでは、自由落下の変位について順を追って見ていきましょう。
変位とは何か
それではまず変位とは何かについて解説していきます。
変位の定義
変位とは、物体の位置の変化をベクトルで表したものです。始点から終点への直線的な位置の変化を示し、向きと大きさを持つ物理量になります。
数式で表すと、変位Δx = x₂ – x₁(x₂は終点の位置、x₁は始点の位置)となります。自由落下では、通常、下向きを正の方向とするため、落下すると変位は正の値になるのです。
変位は単なる数値ではなくベクトル量であるため、向きの情報も含まれています。これが距離との重要な違いでしょう。
変位と距離の違い
変位と距離は似ているようで異なる概念です。変位はベクトル量、距離はスカラー量という根本的な違いがあります。
【変位と距離の違い】
変位:始点から終点への直線的な位置の変化(向きあり)
距離:物体が実際に移動した経路の長さ(向きなし)
自由落下のように一直線上を動く場合、変位の大きさと距離は一致します。しかし、往復運動や曲線運動では両者は異なる値になるのです。
| 項目 | 変位 | 距離 |
|---|---|---|
| 性質 | ベクトル量 | スカラー量 |
| 向き | あり | なし |
| 値 | 正・負・ゼロ | 常に正またはゼロ |
| 単位 | m(メートル) | m(メートル) |
| 自由落下での値 | 距離と同じ | 変位と同じ |
座標系と変位の符号
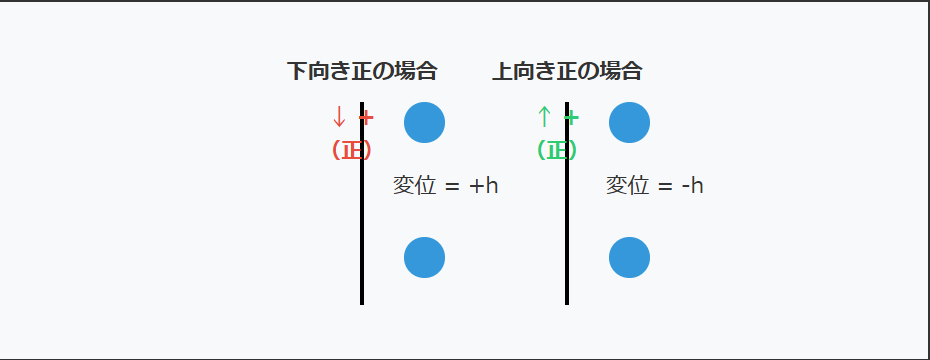
変位の符号は座標系の取り方によって変わります。自由落下では、下向きを正とするか上向きを正とするかを明確にする必要があるのです。
下向きを正の方向とした場合、落下すると変位は正の値になります。逆に上向きを正とした場合、落下すると変位は負の値になるでしょう。どちらの座標系を使っても物理的な現象は同じですが、式の符号が変わります。
変位の公式と求め方
続いては変位の公式と求め方を確認していきます。
基本的な変位の公式
自由落下における変位の基本公式は、h = (1/2)gt²です。これは等加速度運動の変位の公式に、初速度v₀ = 0、加速度a = gを代入したものになります。
【変位の公式の導出】
等加速度運動の一般式:x = v₀t + (1/2)at²
自由落下の条件:v₀ = 0、a = g
代入:h = 0 × t + (1/2)gt²
結果:h = (1/2)gt²
この公式が示すのは、変位が時間の2乗に比例するということです。時間が2倍になると変位は4倍、3倍になると9倍になるという特徴があるでしょう。
時間から変位を求める
落下時間tがわかっているときに変位hを求めるには、公式 h = (1/2)gt² に値を代入して計算します。
【計算例1】物体を自由落下させて3秒後の変位を求めよ。(g = 10 m/s²とする)
【解答】
h = (1/2)gt² = (1/2) × 10 × 3²
= 5 × 9 = 45 m
答え:45メートル
計算する際は、まず時間を2乗してから、重力加速度をかけ、最後に1/2をかけるという順序で行うとよいでしょう。
速度から変位を求める
到達時の速度vがわかっている場合は、v² = 2gh という関係式を変形して h = v²/(2g) で変位を求められます。
【計算例2】自由落下で40 m/sに達したとき、変位はいくらか。(g = 10 m/s²とする)
【解答】
h = v²/(2g) = 40²/(2 × 10)
= 1600/20 = 80 m
答え:80メートル
この方法では、時間を経由せずに直接変位が求められるため便利です。エネルギー保存則からも同じ結果が得られるでしょう。
変位と時間の関係
続いては変位と時間の関係を確認していきます。
時間の2乗に比例する変位
公式 h = (1/2)gt² から、変位は時間の2乗に比例することがわかります。これは等加速度運動の重要な特徴です。
| 時間(秒) | 時間の2乗 | 変位(m) | 変位の比 |
|---|---|---|---|
| 1 | 1 | 5 | 1 |
| 2 | 4 | 20 | 4 |
| 3 | 9 | 45 | 9 |
| 4 | 16 | 80 | 16 |
表からわかるように、時間が等間隔でも変位の増加量は一定ではありません。時間が経つほど単位時間あたりの変位の増加が大きくなるのです。
各秒ごとの変位の増加
連続する1秒間の変位の増加量を見ると、興味深いパターンがあります。増加量が奇数の連続になるという規則性です。
【1秒ごとの変位増加量(g = 10 m/s²)】
0〜1秒:5 m(増加量5 m)
1〜2秒:20 – 5 = 15 m(増加量15 m)
2〜3秒:45 – 20 = 25 m(増加量25 m)
3〜4秒:80 – 45 = 35 m(増加量35 m)
→ 5、15、25、35…(差は10ずつ増加)
この規則性は、ガリレオが斜面の実験で発見したものです。等加速度運動の本質的な性質を示しているでしょう。
平均速度との関係
変位は「平均速度 × 時間」でも表すことができます。自由落下の平均速度は v̄ = (0 + v)/2 = gt/2 なので、h = v̄ × t = (gt/2) × t = (1/2)gt² となるのです。
例えば、3秒後の瞬間速度が30 m/sの場合、平均速度は15 m/sです。したがって変位は 15 × 3 = 45 mとなり、公式から計算した値と一致します。
変位のグラフ
続いては変位のグラフを確認していきます。
変位-時間グラフ(x-tグラフ)
自由落下の変位-時間グラフは、原点を通る放物線(下に凸の曲線)となります。
変位が時間の2乗に比例するため、このような形になるのです。
このグラフの特徴は、時間が経つにつれて傾きが急になっていくことです。これは速度が増加していることを表しているでしょう。
グラフの傾きの意味
x-tグラフの傾きは速度を表します。ある時刻における接線の傾きが、その瞬間の速度となるのです。
数学的には、傾き = dh/dt = v であり、微分によって速度が求められるという関係です。グラフが放物線なので、傾きは時間とともに直線的に増加します。
【グラフの傾きと速度】
t = 0秒:傾き = 0(速度0 m/s)
t = 1秒:傾き = 10(速度10 m/s)
t = 2秒:傾き = 20(速度20 m/s)
t = 3秒:傾き = 30(速度30 m/s)
原点を通らない場合
落下開始位置を地面から高さh₀の位置に設定した場合、グラフは原点を通りません。式は h = h₀ – (1/2)gt² となり、y切片h₀を持つ放物線になるのです。
この場合、時間が経つにつれて変位(地面からの高さ)は減少します。グラフは右下がりの放物線となるでしょう。
変位に関する応用問題
続いては変位に関する応用問題を確認していきます。
途中の変位を求める
落下の途中で特定の時刻における変位を求める問題では、落下開始点を基準に考えます。
【応用例1】高さ100mから物体を落とした。落下開始から2秒後の地面からの高さを求めよ。(g = 10 m/s²)
【解答】
2秒後の変位:h = (1/2) × 10 × 2² = 20 m
地面からの高さ:100 – 20 = 80 m
答え:80メートル
2つの時刻の変位の差
異なる時刻での変位の差を求める問題では、それぞれの時刻での変位を計算してから差をとります。
【応用例2】1秒後と3秒後の変位の差を求めよ。(g = 10 m/s²)
【解答】
1秒後:h₁ = (1/2) × 10 × 1² = 5 m
3秒後:h₂ = (1/2) × 10 × 3² = 45 m
差:45 – 5 = 40 m
答え:40メートル
変位から時間を逆算
変位がわかっているときに時間を求めるには、公式を変形した t = √(2h/g) を使用します。
【応用例3】変位が80mになるのは何秒後か。(g = 10 m/s²)
【解答】
t = √(2h/g) = √(2 × 80 / 10)
= √16 = 4秒
答え:4秒後
まとめ
変位とは物体の位置の変化をベクトルで表したもので、始点から終点への直線的な位置の変化を示します。自由落下における変位は h = (1/2)gt² で求められ、時間の2乗に比例します。
変位と距離の違いは、変位がベクトル量(向きあり)で距離がスカラー量(向きなし)という点です。変位-時間グラフは原点を通る放物線となり、グラフの傾きは速度を表します。
変位の概念を正確に理解することで、運動の記述がより厳密になり、物理学の理解が深まるでしょう。座標系の取り方によって変位の符号が変わることにも注意が必要です。