自由落下において時間を求めることは、物理学の基本的な計算技術の一つです。落下にかかる時間を正確に計算できることは、安全設計や実験計画など、様々な場面で必要とされます。
本記事では、自由落下の時間の求め方と公式を詳しく解説し、距離から時間を計算する方法や、速度から時間を求める方法をご紹介していきます。具体的な計算例を通じて、実践的なスキルを身につけましょう。
それでは、自由落下の時間について順を追って見ていきましょう。
時間を求める基本公式
それではまず時間を求める基本公式について解説していきます。
公式の導出方法
自由落下の時間を求める公式は、基本公式を変形することで得られます。どの公式から導出するかによって、異なる形の時間の式が得られるのです。
距離の公式 h = (1/2)gt² を時間tについて解くと、両辺を2倍して gt² = 2h、さらに両辺をgで割って t² = 2h/g、最後に平方根をとって t = √(2h/g) となります。
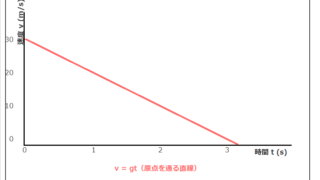
速度の公式 v = gt から時間を求める場合は、両辺をgで割るだけで t = v/g という簡単な形になるでしょう。
【時間を求める2つの公式】
距離hがわかっている場合:t = √(2h/g)
速度vがわかっている場合:t = v/g
(t:時間、h:距離、v:速度、g:重力加速度)
公式の使い分け
問題によって与えられる情報が異なるため、状況に応じて適切な公式を選択する必要があります。何がわかっていて何を求めたいのかを明確にすることが重要です。
| 与えられている情報 | 使用する公式 | 計算の特徴 |
|---|---|---|
| 落下距離(高さ) | t = √(2h/g) | 平方根の計算が必要 |
| 到達時の速度 | t = v/g | 割り算だけで計算可能 |
| 距離と速度の両方 | どちらの公式でもOK | 検算に使える |
公式の意味
時間の公式 t = √(2h/g) は、落下距離の平方根に比例するという関係を表しています。つまり、高さが4倍になっても時間は2倍にしかならないのです。
また、重力加速度gが大きいほど時間は短くなります。月面(g ≒ 1.6 m/s²)では地球の約2.5倍の時間がかかることになるでしょう。
【高さと時間の関係】
高さ5m → 時間1秒(g = 10 m/s²)
高さ20m → 時間2秒(4倍の高さで2倍の時間)
高さ45m → 時間3秒(9倍の高さで3倍の時間)
高さ80m → 時間4秒(16倍の高さで4倍の時間)
距離から時間を求める方法
続いては距離から時間を求める方法を確認していきます。
基本的な計算手順
落下距離がわかっているときに時間を求めるには、公式 t = √(2h/g) を使用します。計算は以下の手順で進めるとよいでしょう。
【計算手順】
ステップ1:2h/g を計算する
ステップ2:その値の平方根をとる
ステップ3:単位を確認する(秒)
例えば、高さ45mから落下する時間を求める場合(g = 10 m/s²)、まず 2 × 45 / 10 = 90 / 10 = 9 を計算し、次に √9 = 3 として、答えは3秒となります。
具体的な計算例
様々な高さでの計算例を見ていきましょう。実際の問題で頻出する値を使って練習することが大切です。
【計算例1】高さ20mから物体を自由落下させた。地面到達までの時間を求めよ。(g = 10 m/s²)
【解答】
t = √(2h/g) = √(2 × 20 / 10)
= √(40/10) = √4 = 2秒
答え:2秒
【計算例2】高さ80mのビルの屋上から物を落とした。地面に到達するまでの時間は?(g = 10 m/s²)
【解答】
t = √(2 × 80 / 10) = √16 = 4秒
答え:4秒
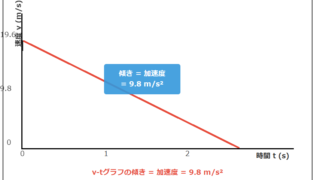
g = 9.8 m/s²を使った計算
より正確な計算が必要な場合は、g = 9.8 m/s²を使用します。この場合、平方根が整数にならないことが多いでしょう。
【計算例3】高さ50mから落下する時間を求めよ。(g = 9.8 m/s²)
【解答】
t = √(2 × 50 / 9.8) = √(100/9.8) = √10.204…
≒ 3.19秒
答え:約3.2秒
このような場合は、小数第2位または第3位で四捨五入して答えることが一般的です。問題文に指定がある場合はそれに従いましょう。
| 高さ(m) | 時間(g=10) | 時間(g=9.8) |
|---|---|---|
| 5 | 1.00秒 | 1.01秒 |
| 20 | 2.00秒 | 2.02秒 |
| 45 | 3.00秒 | 3.03秒 |
| 100 | 4.47秒 | 4.52秒 |
速度から時間を求める方法
続いては速度から時間を求める方法を確認していきます。
速度を使った計算
落下後の速度がわかっているときは、t = v/g という簡単な公式で時間を求められます。割り算だけで済むため、計算が容易です。
【計算例4】自由落下で30 m/sに達するまでの時間を求めよ。(g = 10 m/s²)
【解答】
t = v/g = 30/10 = 3秒
答え:3秒
この公式は v = gt を変形したものです。速度が重力加速度の何倍になっているかを計算していることになるでしょう。
速度と距離の両方がわかる場合
速度と距離の両方がわかっている場合、2つの方法で時間を求められます。これは答えの検算にも利用できるのです。
【例題】物体が45m落下して30 m/sに達した。落下時間を2つの方法で求めよ。(g = 10 m/s²)
【方法1:距離から】
t = √(2h/g) = √(2 × 45 / 10) = √9 = 3秒
【方法2:速度から】
t = v/g = 30/10 = 3秒
両方の方法で同じ答えが得られる!
もし2つの方法で異なる答えが出た場合は、どこかで計算ミスをしている可能性があります。このような検算方法を知っておくと便利でしょう。
平均速度を使った方法
自由落下では、平均速度v̄ = v/2 = gt/2 という関係があります。これを利用しても時間を求めることができるのです。
距離は「平均速度 × 時間」でも表せるため、h = v̄ × t = (gt/2) × t = (1/2)gt² となります。この式から t = √(2h/g) が導けるでしょう。
平均速度を使った考え方は、直感的に理解しやすい場合があります。例えば、0 m/sから30 m/sまで加速する場合、平均速度は15 m/sです。
時間に関する応用問題
続いては時間に関する応用問題を確認していきます。
途中経過を求める問題
落下の途中で特定の条件を満たす時刻を求める問題もあります。段階的に考えることが重要です。
【応用例1】高さ100mから物体を落とした。落下開始から20m落ちるまでの時間を求めよ。(g = 10 m/s²)
【解答】
20m落下する時間を求める
t = √(2 × 20 / 10) = √4 = 2秒
答え:2秒
このような問題では、落下開始点を基準にして考えます。「残り80m」ではなく「20m落ちた」という条件に着目するのです。
時間差を求める問題
2つの異なる地点を通過する時間の差を求める問題も出題されます。それぞれの時刻を求めてから、差を計算しましょう。
【応用例2】高さ80mから落下した物体が、高さ60mの地点と高さ20mの地点を通過する時間の差を求めよ。(g = 10 m/s²)
【解答】
高さ60mの地点(20m落下):t₁ = √(40/10) = 2秒
高さ20mの地点(60m落下):t₂ = √(120/10) = √12 ≒ 3.46秒
時間差:3.46 – 2 = 1.46秒
答え:約1.5秒
複数の物体の比較
異なる高さから落とした複数の物体の落下時間を比較する問題では、時間の比が高さの平方根の比になることを利用できます。
【比の利用】
高さの比が 1 : 4 : 9 なら
時間の比は 1 : 2 : 3
(√1 : √4 : √9 = 1 : 2 : 3)
| 物体 | 高さ(m) | 時間(秒) | 時間の比 |
|---|---|---|---|
| A | 5 | 1 | 1 |
| B | 20 | 2 | 2 |
| C | 45 | 3 | 3 |
| D | 80 | 4 | 4 |
実用的な時間計算
続いては実用的な時間計算を確認していきます。
反応時間を含む計算
実際の状況では、人間の反応時間も考慮する必要があります。落下時間に反応時間を加えることで、実際に必要な時間がわかるのです。
【実用例】高さ5mの場所から物が落ちるのを見て避ける場合
落下時間:t = √(2 × 5 / 10) = 1秒
人の反応時間:約0.2〜0.3秒
避けるための動作時間:約0.5秒
必要な時間合計:約0.7〜0.8秒
結論:1秒以内に避ける必要があり、ギリギリ
安全基準への応用
建設現場や工場での安全基準を設定する際、落下時間の計算が使われます。警報装置の作動タイミングなどを決める際に重要です。
例えば、高さ10mからの落下物を検知して警報を鳴らす場合、落下時間は約1.4秒です。検知から警報までに0.2秒かかるとすると、作業員が避けるための時間は約1.2秒しかありません。
スポーツへの応用
スポーツ科学でも落下時間の計算が使われます。例えば、バスケットボールのシュートやバレーボールのスパイクなどの分析に役立つのです。
【バスケットボールの例】
ボールがリングの高さ3.05mから落ちる時間
t = √(2 × 3.05 / 9.8) = √0.622 ≒ 0.79秒
リバウンドを取るための位置取りの参考になる
まとめ
自由落下の時間は、距離がわかっている場合は t = √(2h/g)、速度がわかっている場合は t = v/g という公式で求められます。時間は距離の平方根に比例し、高さが4倍になっても時間は2倍にしかなりません。
計算の際は、2h/gを先に計算してから平方根をとる手順で進め、g = 10 m/s²を使うと計算が簡単になります。速度と距離の両方がわかっている場合は、2つの方法で時間を求めて検算することができるでしょう。
実用的な問題では反応時間や動作時間も考慮し、安全基準の設定やスポーツ分析など様々な分野で時間計算が応用されています。