物体がどのくらいの距離を落下するかを計算することは、物理学の基本的なスキルです。建築現場での安全対策や、スポーツ競技の記録分析など、実生活でも応用される重要な知識となります。
本記事では、自由落下の距離の求め方と公式を詳しく解説し、時間から距離を計算する方法や、高さに関する様々な問題の解き方をご紹介していきます。具体的な計算例を通じて、理解を深めていきましょう。
それでは、自由落下の距離について順を追って見ていきましょう。
自由落下の距離の公式
それではまず自由落下の距離の公式について解説していきます。
基本公式の導出
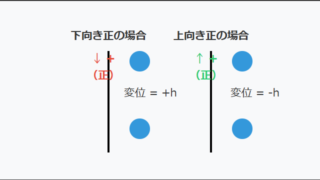
自由落下の距離(変位)を表す基本公式は h = (1/2)gt²です。この式は、等加速度運動の一般式から導出できます。
等加速度運動の変位の公式は x = v₀t + (1/2)at² であり、自由落下では初速度v₀ = 0、加速度a = gを代入することで、h = (1/2)gt² が得られるのです。
この公式が示すのは、落下距離が時間の2乗に比例するということです。時間が2倍になると距離は4倍、3倍になると9倍になるという特徴があるでしょう。
【距離の公式の導出】
等加速度運動の一般式:x = v₀t + (1/2)at²
自由落下の条件:v₀ = 0、a = g
代入すると:h = 0 × t + (1/2)gt²
結果:h = (1/2)gt²
公式に含まれる記号の意味
公式 h = (1/2)gt² に含まれる各記号の意味を正確に理解することが重要です。それぞれの物理量が何を表しているかを確認しましょう。
| 記号 | 名称 | 単位 | 意味 |
|---|---|---|---|
| h | 落下距離(高さ) | m(メートル) | 落下した距離 |
| g | 重力加速度 | m/s² | 約9.8 m/s² |
| t | 時間 | s(秒) | 落下にかかった時間 |
計算する際は、単位を統一することが重要です。距離をメートル、時間を秒、加速度をm/s²で表せば、単位の整合性が保たれるでしょう。
公式の変形
基本公式 h = (1/2)gt² を変形することで、時間tや重力加速度gを求めることもできます。問題に応じて適切な形に変形して使用するのです。
【公式の変形例】
距離を求める:h = (1/2)gt²
時間を求める:t = √(2h/g)
加速度を求める:g = 2h/t²
例えば、落下距離と重力加速度がわかっているときに落下時間を求めたい場合は、t = √(2h/g) という形に変形した公式を使うと便利でしょう。
時間から距離を計算する方法
続いては時間から距離を計算する方法を確認していきます。
基本的な計算手順
時間tがわかっているときに落下距離hを求めるには、公式 h = (1/2)gt² に値を代入して計算します。計算の手順を段階的に追うことで、ミスを減らせるでしょう。
【計算例1】物体を自由落下させたところ、3秒後に地面に到達した。落下距離を求めよ。(g = 10 m/s²とする)
【解答】
与えられた値:t = 3秒、g = 10 m/s²
公式に代入:h = (1/2) × 10 × 3²
計算:h = 5 × 9 = 45 m
答え:45メートル
計算する際は、まず時間を2乗してから、重力加速度をかけ、最後に1/2をかけるという順序で行うとよいでしょう。
異なる時間での比較
異なる時間で落下した場合の距離を比較すると、時間の2乗に比例する関係が明確になります。この関係を理解することで、計算の検算にも役立つのです。
| 時間(秒) | 計算式(g=10m/s²) | 落下距離(m) | 比 |
|---|---|---|---|
| 1 | (1/2)×10×1² | 5 | 1 |
| 2 | (1/2)×10×2² | 20 | 4 |
| 3 | (1/2)×10×3² | 45 | 9 |
| 4 | (1/2)×10×4² | 80 | 16 |
表からわかるように、時間が2倍になると距離は4倍、3倍になると9倍になります。この法則を知っていると、計算結果が妥当かどうかを素早く判断できるでしょう。
g = 9.8 m/s²を使った計算
より正確な計算が必要な場合は、g = 9.8 m/s²を使用します。計算がやや複雑になりますが、実際の現象により近い値が得られるのです。
【計算例2】2秒間自由落下した物体の落下距離を求めよ。(g = 9.8 m/s²とする)
【解答】
h = (1/2) × 9.8 × 2²
h = (1/2) × 9.8 × 4
h = 4.9 × 4 = 19.6 m
答え:19.6メートル
g = 10 m/s²を使った場合の答え(20m)と比べると、約2%の差があります。精密な計算が求められる場合は、g = 9.8 m/s²を使うべきでしょう。
距離から時間や速度を求める方法
続いては距離から時間や速度を求める方法を確認していきます。
落下距離から時間を求める
落下距離hがわかっているときに時間tを求めるには、公式を変形した t = √(2h/g) を使用します。平方根の計算が必要になるため、電卓を使うとよいでしょう。
【計算例3】高さ20mから物体を自由落下させた。地面に到達するまでの時間を求めよ。(g = 10 m/s²とする)
【解答】
与えられた値:h = 20 m、g = 10 m/s²
公式に代入:t = √(2 × 20 / 10)
計算:t = √(40/10) = √4 = 2秒
答え:2秒
この計算では、まず2h/gを計算してから平方根をとります。平方根が整数にならない場合もあるため、その場合は小数で答えるか、√の形のまま答えるとよいでしょう。
落下距離から速度を求める
落下距離がわかっているときに、地面到達直前の速度を求めることもできます。速度と距離の関係式 v² = 2gh を使用するのです。
【計算例4】高さ45mから物体を自由落下させた。地面に到達する直前の速度を求めよ。(g = 10 m/s²とする)
【解答】
公式 v² = 2gh に代入
v² = 2 × 10 × 45 = 900
v = √900 = 30 m/s
答え:30 m/s
この方法では、時間を経由せずに直接速度が求められるため、計算が簡単になります。エネルギー保存則を使っても同じ結果が得られるでしょう。
実用的な問題への応用
実際の問題では、複数のステップを組み合わせて解く必要がある場合もあります。与えられた条件を整理し、適切な公式を選択することが重要です。
【応用例】ビルの屋上から石を落としたところ、地面に到達する直前の速度が40 m/sだった。ビルの高さを求めよ。(g = 10 m/s²とする)
【解答】
v² = 2gh より h = v²/(2g)
h = 40²/(2 × 10) = 1600/20 = 80 m
答え:80メートル
高さに関する様々な計算
続いては高さに関する様々な計算を確認していきます。
途中の高さでの速度
物体が特定の高さを通過するときの速度を求める問題もよく出題されます。落下開始点からの距離を使って計算するのです。
【例題】高さ100mから物体を自由落下させた。落下開始から20m落ちた地点での速度を求めよ。(g = 10 m/s²とする)
【解答】
20m落下した時点での速度を求める
v² = 2gh = 2 × 10 × 20 = 400
v = √400 = 20 m/s
答え:20 m/s
このように、落下開始点からの距離を基準に計算します。残りの高さ(80m)ではなく、すでに落ちた距離(20m)を使うことに注意しましょう。
複数の物体の比較
異なる高さから落とした複数の物体を比較する問題も重要です。それぞれの物体について個別に計算し、結果を比較します。
| 高さ(m) | 到達時間(秒) | 到達速度(m/s) |
|---|---|---|
| 5 | 1 | 10 |
| 20 | 2 | 20 |
| 45 | 3 | 30 |
| 80 | 4 | 40 |
このように整理すると、高さが4倍になると時間は2倍、速度も2倍になることがわかるでしょう。これは h ∝ t²、v ∝ t という関係から導かれる結果です。
安全基準への応用
自由落下の計算は、建設現場や工場での安全基準を決める際にも使われます。落下物の危険性を評価するために、速度やエネルギーを計算するのです。
例えば、高さ10mからの落下物は約14 m/s(時速約50km)で地面に到達します。これは自動車が衝突するのと同程度の衝撃力を持つため、ヘルメット着用などの安全対策が必要となります。
労働安全衛生規則では、2m以上の高所作業では墜落制止用器具の使用が義務付けられています。これは2mからの落下でも約6.3 m/sの速度に達し、危険であるためです。
まとめ
自由落下の距離は h = (1/2)gt² という公式で求められ、距離は時間の2乗に比例します。時間がわかっていれば直接代入して距離を計算でき、逆に距離がわかっていれば t = √(2h/g) で時間を求められます。
速度と距離の関係式 v² = 2gh を使えば、時間を経由せずに速度と距離を関連付けることができます。g = 10 m/s²を使うと計算が簡単になり、g = 9.8 m/s²を使うとより正確な値が得られるでしょう。
これらの公式と計算方法を理解することで、物理の問題だけでなく、実生活での安全評価にも応用できる実用的なスキルが身につきます。