自由落下を理解する上で最も重要な概念の一つが加速度です。すべての物体が同じ速さで落ちるという驚くべき事実は、加速度が一定であることから導かれます。
本記事では、自由落下の加速度について詳しく解説し、重力加速度の値や求め方、加速度が一定である理由について説明していきます。加速度のグラフや計算方法についても具体例を交えてご紹介しましょう。
それでは、自由落下の加速度について順を追って見ていきましょう。
自由落下の加速度とは
それではまず自由落下の加速度とはについて解説していきます。
加速度の基本的な意味
加速度とは、速度の時間変化率のことです。つまり、単位時間あたりにどれだけ速度が変化するかを表す物理量になります。
数式で表すと、加速度a = Δv/Δt = (v₂ – v₁)/(t₂ – t₁) となります。速度が増加する場合は正の加速度、減少する場合は負の加速度(減速)となるのです。
加速度の単位はm/s²(メートル毎秒毎秒)です。これは「1秒ごとに速度が何m/s増加するか」を意味しているでしょう。例えば、加速度が5m/s²なら、1秒ごとに速度が5m/sずつ増加することになります。
重力加速度とは
自由落下における加速度を特に重力加速度と呼びます。記号gで表され、地球上ではほぼ一定の値を持つのです。
重力加速度は地球が物体を引きつける力によって生じる加速度であり、地球上のあらゆる物体に等しく働きます。質量の大小に関わらず、すべての物体が同じ加速度で落下するという驚くべき性質を持っているでしょう。
【重力加速度の値】
標準重力加速度:g = 9.80665 m/s²
一般的な近似値:g ≒ 9.8 m/s²
計算での簡略値:g ≒ 10 m/s²
※物理の問題では、指定がなければg = 9.8 m/s²または10 m/s²を使用
加速度が一定である理由
自由落下では、加速度が常に一定値gに保たれます。これは運動方程式ma = mgから導かれる重要な性質です。
両辺をmで割るとa = gとなり、質量mが約分されて消えるため、加速度は質量によらず常にgとなるのです。1kgの物体も100kgの物体も、同じ加速度gで落下します。
また、落下中に速度が変化しても、働く力(重力mg)は変わらないため、加速度も変化しません。これが等加速度運動と呼ばれる理由でしょう。
| 時刻(秒) | 速度(m/s) | 加速度(m/s²) |
|---|---|---|
| 0 | 0 | 9.8 |
| 1 | 9.8 | 9.8 |
| 2 | 19.6 | 9.8 |
| 3 | 29.4 | 9.8 |
重力加速度の値と地域差
続いては重力加速度の値と地域差を確認していきます。
標準重力加速度
国際的に定められた標準重力加速度は、g = 9.80665 m/s²です。この値は海面上、緯度45度の地点における重力加速度として定義されています。
日本の物理教育では、通常g = 9.8 m/s²を使用します。より簡単な計算のために、g = 10 m/s²と近似することもあるでしょう。問題文に特に指定がない場合は、9.8 m/s²または10 m/s²を使うのが一般的です。
厳密な計算が必要な場合は9.8 m/s²、概算や暗算で解く場合は10 m/s²を使い分けると効率的でしょう。
地域による重力加速度の違い
重力加速度は地球上の位置によってわずかに変化します。主な要因は、地球の自転による遠心力と、地球が完全な球形でないことです。
赤道付近では遠心力が大きいため重力加速度は小さくなり、約9.78 m/s²となります。一方、極地方では遠心力がほとんど働かないため、約9.83 m/s²と大きくなるのです。
【地域別の重力加速度】
赤道付近:約9.78 m/s²
東京:約9.798 m/s²
標準値(緯度45度):9.80665 m/s²
極地方:約9.83 m/s²
※差は約0.5%程度で、通常の計算では無視できる
高度による変化
重力加速度は地球の中心からの距離に依存するため、高度が上がると重力加速度はわずかに減少します。万有引力の法則により、距離の2乗に反比例して重力は弱くなるのです。
ただし、日常的な高度の範囲(数千メートル程度)では、変化は非常にわずかです。例えば、標高1000mでの重力加速度は地上より約0.03%小さくなる程度でしょう。
国際宇宙ステーション(ISS)が周回する高度400km付近では、重力加速度は地表の約88%(約8.6 m/s²)まで減少します。しかし、ISSが無重力状態なのは高度が高いからではなく、自由落下し続けているためです。
加速度の求め方と計算方法
続いては加速度の求め方と計算方法を確認していきます。
運動方程式から求める方法
自由落下の加速度は、運動方程式ma = mgから直接求められます。両辺をmで割ることで、a = gという関係が得られるのです。
この方法は理論的なアプローチであり、加速度が重力加速度gに等しいことを証明するものです。実際の数値を求める際には、gの値を代入すればよいでしょう。
【運動方程式からの導出】
ステップ1:運動方程式を立てる F = ma
ステップ2:自由落下では F = mg
ステップ3:ma = mg
ステップ4:両辺をmで割る a = g
結論:自由落下の加速度は重力加速度gに等しい
速度の変化から求める方法
実験的に加速度を求める場合、速度の時間変化を測定して計算します。加速度a = Δv/Δt = (v₂ – v₁)/(t₂ – t₁) という定義式を使うのです。
例えば、落下開始から1秒後の速度が9.8 m/s、2秒後の速度が19.6 m/sだった場合、加速度は a = (19.6 – 9.8)/(2 – 1) = 9.8 m/s² と計算できるでしょう。
【計算例】
時刻t₁ = 1秒のとき速度v₁ = 9.8 m/s
時刻t₂ = 3秒のとき速度v₂ = 29.4 m/s
加速度 a = (29.4 – 9.8)/(3 – 1) = 19.6/2 = 9.8 m/s²
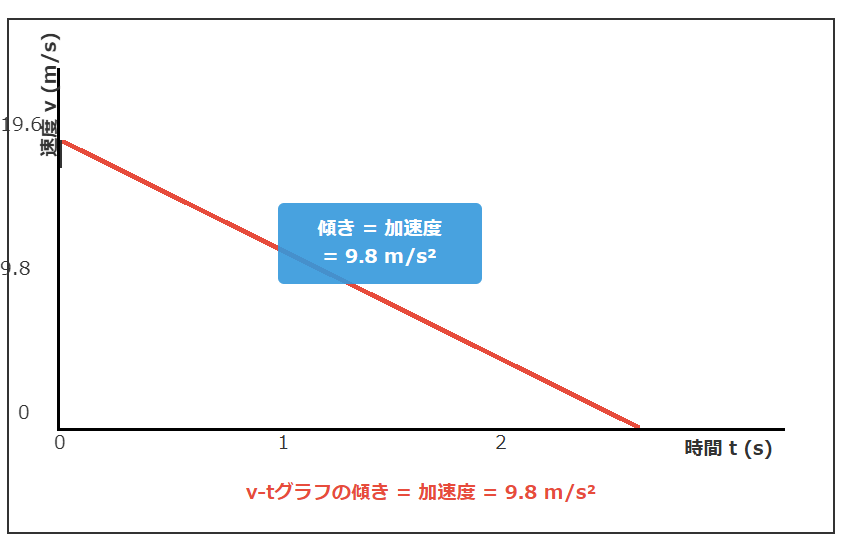
グラフから求める方法
速度-時間グラフ(v-tグラフ)の傾きは加速度を表します。自由落下のv-tグラフは原点を通る直線なので、この直線の傾きが重力加速度gとなるのです。
= 9.8 m/s²
グラフ上の2点を選び、傾き = (縦の変化量)/(横の変化量)を計算すれば加速度が求まります。どの2点を選んでも同じ値になることが、加速度が一定であることの証明にもなるでしょう。
加速度のグラフと特徴
続いては加速度のグラフと特徴を確認していきます。
加速度-時間グラフ(a-tグラフ)
自由落下の加速度-時間グラフは、時間軸に平行な水平線となります。これは加速度が常に一定値g(約9.8 m/s²)であることを視覚的に示しています。
このグラフの面積は速度の変化量を表します。例えば、0秒から3秒までの面積は 9.8 × 3 = 29.4 m/s となり、3秒間で速度が29.4 m/s増加したことがわかるでしょう。
他の運動との比較
自由落下以外の運動では、加速度が異なる振る舞いをします。加速度のグラフを比較することで、運動の特徴がより明確になるのです。
| 運動の種類 | 加速度 | a-tグラフの形 |
|---|---|---|
| 自由落下 | 一定(g) | 水平な直線 |
| 等速直線運動 | ゼロ | a = 0の直線 |
| 空気抵抗あり落下 | 減少(g→0) | 右下がりの曲線 |
| 等加速度運動(一般) | 一定 | 水平な直線 |
加速度が一定であることの重要性
加速度が一定であることは、運動を簡単な公式で記述できるという大きな利点をもたらします。これが等加速度運動の特徴です。
加速度が一定なら、速度は時間に比例し(v = gt)、変位は時間の2乗に比例する(x = (1/2)gt²)という単純な関係が成り立ちます。もし加速度が時間によって変化すると、これほど簡単には記述できないでしょう。
加速度が一定であることは、自由落下が「最も基本的な運動の一つ」として物理教育で重視される理由です。数学的に扱いやすく、かつ実際の現象をよく近似できるのです。
まとめ
自由落下の加速度は重力加速度gであり、その値は標準で9.80665 m/s²、一般的には9.8 m/s²または10 m/s²として扱われます。この加速度は物体の質量によらず常に一定であり、運動方程式ma = mgから a = g として導出できます。
重力加速度は地域や高度によってわずかに変化しますが、通常の計算では無視できる程度です。加速度は速度の時間変化率として Δv/Δt で求められ、v-tグラフの傾きとしても表されます。a-tグラフは時間軸に平行な水平線となり、加速度が一定であることを視覚的に示すのです。
加速度が一定であることにより、自由落下は等加速度運動として簡潔な公式で記述でき、物理学習の基礎となる重要な運動となっています。