数学の組み合わせ計算で登場する「9C1」という表記。これは組み合わせの中でも最もシンプルで基本的な形の一つです。
9個のものから1個だけを選ぶ組み合わせを表す9C1は、直感的にも理解しやすい問題でしょう。しかし、公式を使った正確な計算方法や、なぜその答えになるのかを論理的に説明できることが重要になります。
この記事では、9C1の具体的な計算方法から答えまでを丁寧に解説していきます。さらに、9C1と9C8が同じ値になるという興味深い性質や、組み合わせ計算全般に使える覚え方のコツについても詳しく説明しますね。
確率や場合の数を求める際に必須となる組み合わせの考え方。9C1という基本的な問題を通じて、組み合わせの本質的な理解を深めていきましょう。それでは早速、9C1の答えと基本的な意味から確認していきます。
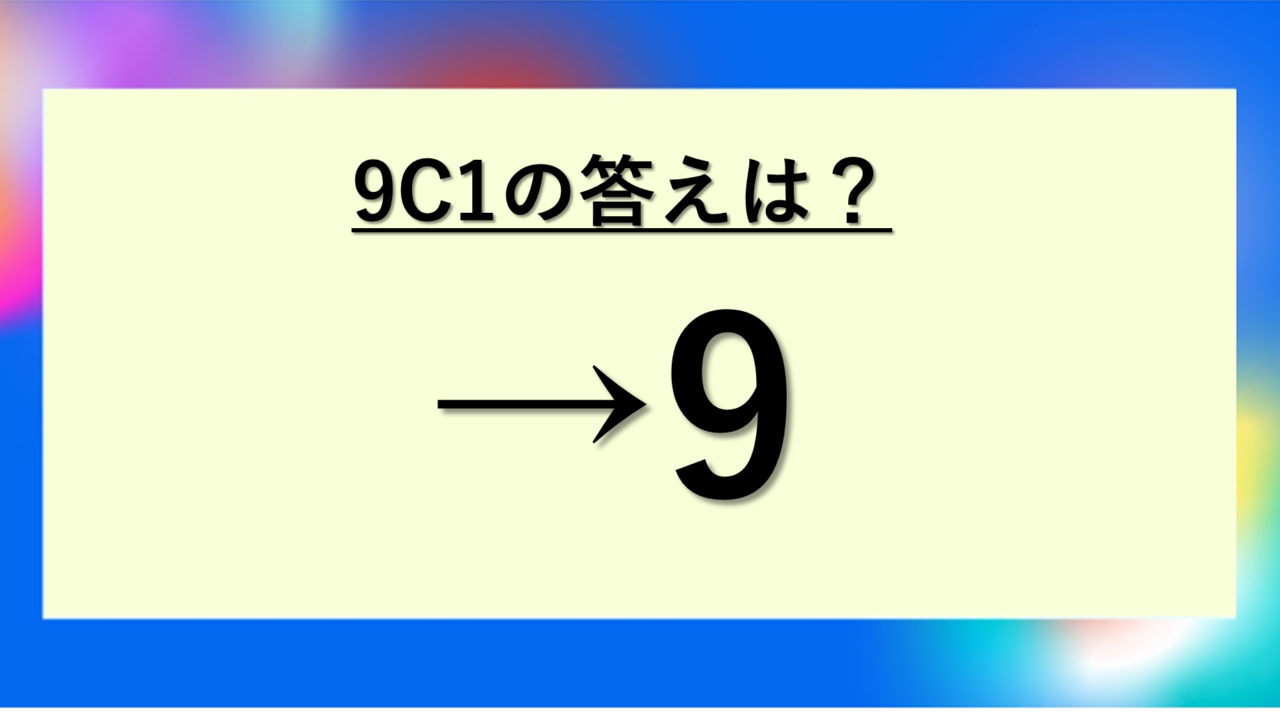
9C1の答えは9!組み合わせの基本原理を理解しよう
それではまず、9C1の計算結果とその基本的な意味について解説していきます。
9C1の答えとその数学的な意味
この答えは、9個のものから1個を選ぶ組み合わせの総数を表しています。9個の選択肢があれば、そのうちどれか1つを選ぶ方法は9通りあるという、非常に直感的な結果ですね。
例えば、9人の候補者から1人の代表を選ぶ場合、選び方は9通りになります。AさんからIさんまで9人いれば、誰を選ぶかによって9通りの選び方が存在するのです。
9C1は組み合わせの中でも最も基本的なパターンの一つであり、この理解が他の複雑な組み合わせ計算の基礎となるでしょう。

nC1という基本パターンの意味
9C1は、一般形で表すとnC1という形になります。これは「n個の中から1個を選ぶ組み合わせ」を表す基本的なパターンです。
nC1の答えは、nがどんな数であっても常にnになります。5C1なら5、10C1なら10、100C1なら100という具合です。この規則性を理解しておくと、瞬時に答えを導き出せるようになるでしょう。
「C」は英語の「Combination(組み合わせ)」の頭文字から来ており、順序を考慮しない選び方を表します。読み方は「9シー1」または「9コンビネーション1」となりますね。
9C1が表す具体的な状況
9C1は日常生活の様々な場面で活用できる考え方です。
例えば、9種類のアイスクリームから1種類を選ぶ場合の選び方が9C1になります。また、9冊の本の中から1冊を購入する際の選び方も同様に9C1で表現できるでしょう。
このような状況では、どれを選ぶかだけが問題であり、選ぶ順序は関係ありません。これが組み合わせ(C)の特徴です。もし選ぶ順序が重要なら順列(P)を使うことになりますが、9C1のケースでは1個しか選ばないため、順序の概念そのものが存在しないのです。
確率の問題でも、「9個の中から1個を選ぶ」という状況は頻繁に登場します。9C1の理解は、確率計算の基礎となる重要なスキルでしょう。
9C1の計算方法と求め方
続いては9C1の具体的な計算方法を確認していきます。
組み合わせの基本公式を使った計算
組み合わせの計算には、次の基本公式を使用します。
9C1 = 9! / (1! × 8!)
ここで「!」は階乗を表す記号です。階乗とは、その数から1まで順に掛け算していく計算方法を意味します。
例えば9! = 9×8×7×6×5×4×3×2×1となりますが、実際の計算ではすべての階乗を展開する必要はありません。効率的な約分のテクニックを使えば、驚くほど簡単に計算できるのです。
実際の計算プロセス
9C1を公式に従って効率的に計算する手順を見ていきましょう。
= (9 × 8!) / (1 × 8!)
= 9 / 1
= 9
この計算では、分子と分母に共通する8!を約分しています。9!は9×8!と書き換えられるため、8!の部分が約分で消えるのです。
分母の1!は1となり、分子には9だけが残ります。最後に9÷1を計算して答えの9が得られるわけですね。大きな階乗を計算せずに済む点がポイントになります。
このように、nC1の形では常に分子にnだけが残り、分母が1になるため、答えは必ずnになるのです。
直感的理解との一致
公式による計算結果が、直感的な理解と完全に一致することを確認しておきましょう。
| アプローチ | 考え方 | 結果 |
|---|---|---|
| 直感的理解 | 9個から1個選ぶ方法は9通り | 9通り |
| 公式計算 | 9! / (1! × 8!) = 9 | 9通り |
| 具体例 | A,B,C,D,E,F,G,H,Iから1つ選ぶ | 9通り |
どの視点から考えても答えが9になることが分かります。数学の公式は直感と一致するように設計されているため、計算結果が常識的な感覚と合っているかを確認する習慣をつけると良いでしょう。
9個の選択肢があれば、そのうちどれか1つを選ぶ方法が9通りあるという、この当たり前の事実が、公式によって正確に導き出されているのです。
9C1と9C8が同じ値になる理由
続いては9C1と9C8の関係性について確認していきます。
補集合の関係による対称性
実は、9C1と9C8はどちらも答えが9で完全に一致します。これは偶然ではなく、組み合わせの持つ本質的な性質なのです。
nCr = nC(n-r)9C1 = 9C(9-1) = 9C8 = 9
この性質が成り立つ理由は、「9個から1個を選ぶ」ことと「9個から8個を選ぶ(1個を残す)」ことが実質的に同じ意味を持つからです。
1個を選ぶということは、裏を返せば8個を選ばないということ。逆に8個を選ぶということは、1個を選ばないということになります。この表裏一体の関係が、9C1と9C8が等しくなる理由なのです。
9C8の計算で検証
9C8を実際に計算して、本当に9になるか確認してみましょう。
= (9 × 8!) / (8! × 1)
= 9 / 1
= 9
計算過程を見ると、9C1とまったく同じ形になることが分かります。分子には9が残り、分母は1となる点も完全に一致していますね。
9C8は「9個から8個を選ぶ方法の数」を意味しますが、これは言い換えると「9個から1個を除外する方法の数」となります。9個のうちどれか1個を除外するかを決めれば、残りの8個は自動的に決まるため、選び方は9通りになるのです。
対称性を活用した計算の工夫
組み合わせの対称性を理解すると、計算効率が大幅に向上します。
一般的な戦略として、rとn-rを比較して小さい方の数で計算すると楽になります。9C8の場合、8よりも1の方が小さいため、9C1として計算した方が圧倒的に簡単です。
| 元の組み合わせ | 変換後 | 計算の簡単さ |
|---|---|---|
| 9C8 | 9C1 | 1!より8!の方が簡単 |
| 10C9 | 10C1 | 瞬時に10と分かる |
| 50C49 | 50C1 | 瞬時に50と分かる |
| 100C99 | 100C1 | 瞬時に100と分かる |
この対称性の理解により、nC(n-1)という形の組み合わせは常にnになることが分かります。99個から98個選ぶ方法も、1000個から999個選ぶ方法も、すべて元の個数nと同じになるのです。
この性質を活用すれば、複雑に見える問題も瞬時に解けるようになるでしょう。テストや入試では大きな時間短縮につながりますね。
組み合わせ計算の覚え方とコツ
続いては組み合わせ計算をマスターするためのコツを確認していきます。
基本パターンの完全暗記
組み合わせには、覚えておくと非常に便利な基本パターンがいくつか存在します。
– nC1 = n (1個選ぶ方法はn通り)
– nC2 = n(n-1)/2 (2個選ぶ公式)
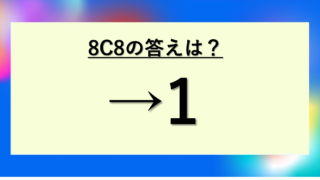
– nCn = 1 (全部選ぶ方法は1通り)
– nC(n-1) = n (n-1個選ぶ方法はn通り)
9C1はこの中のnC1のパターンに該当します。このパターンを覚えておけば、どんなnであっても瞬時に答えが分かるようになるでしょう。
特にnC1とnC(n-1)がどちらもnになるという対称性は重要です。この2つはセットで覚えると効果的ですね。
公式の意味を理解する重要性
組み合わせの公式を単に暗記するのではなく、意味を理解しながら覚えることが重要になります。
nCr = n! / (r! × (n-r)!) という公式は、次のように理解できます。n個のものを1列に並べる方法はn!通りありますが、組み合わせでは順序を考慮しません。そのため、選んだr個の内部での並び替え(r!通り)と、選ばなかったn-r個の内部での並び替え((n-r)!通り)で割る必要があるのです。
9C1の場合、9!を(1!×8!)で割ることで、順序を無視した純粋な「選び方」だけが残ります。この理屈を理解すれば、公式を忘れても自分で導き出せる力が身につくでしょう。
順列(P)との明確な区別
組み合わせ(C)と順列(P)の違いを正確に理解することが、問題を解く上で極めて重要です。
| 項目 | 組み合わせ(C) | 順列(P) |
|---|---|---|
| 順序 | 考慮しない | 考慮する |
| 9個から1個選ぶ | 9C1 = 9通り | 9P1 = 9通り |
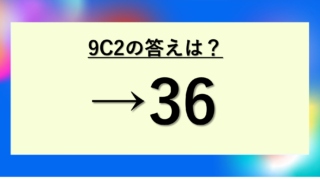
| 9個から2個選ぶ | 9C2 = 36通り | 9P2 = 72通り |
| 公式 | n!/(r!(n-r)!) | n!/(n-r)! |
興味深いことに、1個だけ選ぶ場合は9C1も9P1も同じ9になります。これは、1個しか選ばないため並べる順序が存在せず、組み合わせと順列が一致するからです。
しかし、2個以上選ぶ場合は大きく異なってきます。9C2が36通りであるのに対し、9P2は72通りと2倍になるのです。問題文に「選ぶ」とあれば組み合わせ、「並べる」「配置する」とあれば順列を使うという基本を押さえておきましょう。
9C1に関連する応用問題と考え方
続いては9C1を題材にした応用的な考え方を確認していきます。
確率計算での9C1の活用
9C1は確率問題の場面で頻繁に登場します。
例えば、9個のくじがあり、そのうち1個だけが当たりの場合を考えてみましょう。1回だけくじを引いたときに当たる確率は、当たりくじを選ぶ組み合わせを全体の組み合わせで割ることで求められます。
確率問題の例9個のくじ(当たり1個、はずれ8個)から1個引く
当たる確率 = 1C1 / 9C1 = 1 / 9
はずれる確率 = 8C1 / 9C1 = 8 / 9
このように、9C1は確率の分母として頻繁に使われるのです。全体が9個で1個を選ぶ状況では、必ず9C1 = 9が分母になります。
確率計算における組み合わせの理解は、統計学や確率論の基礎となる重要なスキルでしょう。
場合の数における基本単位
9C1は場合の数を数え上げる問題において、最も基本的な単位となります。
9人のクラスから1人の日直を選ぶ方法、9種類の色から1色を選ぶ方法、9枚のカードから1枚を引く方法など、あらゆる「1つを選ぶ」状況で9C1が活用できるでしょう。
また、より複雑な組み合わせ問題を分解する際にも、nC1という基本パターンの理解が役立ちます。例えば、9個から3個を選ぶ問題を段階的に考える際、まず1個目を選ぶ(9C1)、次に2個目を選ぶという具合に分解できるのです。
パスカルの三角形との関連
9C1は、パスカルの三角形という美しい数学的構造の中にも登場します。
パスカルの三角形は、組み合わせの数を三角形状に配置したもので、各段のn行目にはnC0, nC1, nC2, …という値が並びます。9行目を見ると、9C1の位置には9という数が現れるのです。
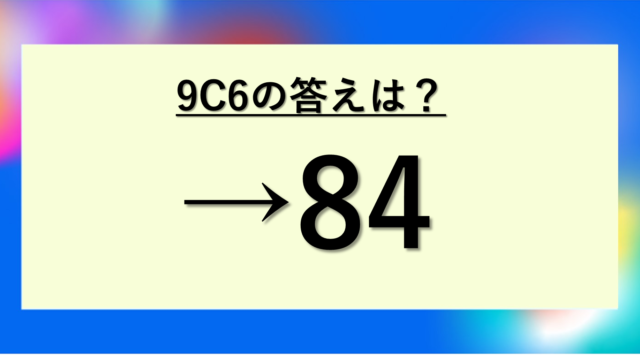
1 9 36 84 …
パスカルの三角形には「隣り合う2つの数を足すと下の段の数になる」という性質があります。この性質により、組み合わせの値を効率的に計算できる場合もあるでしょう。
9C1の理解は、このような数学的な美しい構造を理解する入り口にもなるのです。
まとめ
9C1の計算方法と答えについて詳しく解説してきました。
9C1の答えは9であり、これは9個のものから1個を選ぶ組み合わせの総数を表します。公式nCr = n! / (r! × (n-r)!)を使って計算すると、9! / (1! × 8!)となり、効率的に約分することで9という答えが導き出されるのです。
特に重要なポイントは、9C1と9C8が同じ値になるという対称性でしょう。9個から1個を選ぶことと、9個から8個を選ぶ(1個を残す)ことは実質的に同じ操作であり、この理解が組み合わせの本質を捉える鍵となります。
また、nC1 = nという基本パターンを覚えておくことで、どんな数でも瞬時に答えを導き出せるようになります。組み合わせの計算は、確率や場合の数を求める際の基礎となる重要なスキルです。
この記事で紹介した計算方法やコツを実践することで、9C1のような基本的な組み合わせ計算を確実にマスターし、より複雑な問題にも自信を持って取り組めるようになるでしょう。数学の実力向上に向けて、一歩ずつ着実に理解を深めていきましょう。