組み合わせの計算で「8C7」という表記を見たとき、どのように計算すればよいのか迷ってしまう方も多いのではないでしょうか。
8個のものから7個を選ぶ組み合わせを表す8C7は、一見複雑に思えますが、実は非常にシンプルな計算で答えを導き出せます。組み合わせの基本的な性質を理解すれば、誰でも簡単に計算できるようになるのです。
この記事では、8C7の具体的な計算方法から答えまでを丁寧に解説していきます。さらに、8C7と8C1が同じ値になるという興味深い関係性や、組み合わせ計算全般に使える覚え方のコツについても詳しく説明しますね。
確率や場合の数を求める際に欠かせない組み合わせの計算。8C7を題材にして、組み合わせの本質的な理解を深めていきましょう。それでは早速、8C7の答えと基本的な意味から確認していきます。
8C7の答えは8!組み合わせの基本原理を理解しよう
それではまず、8C7の計算結果とその基本的な意味について解説していきます。
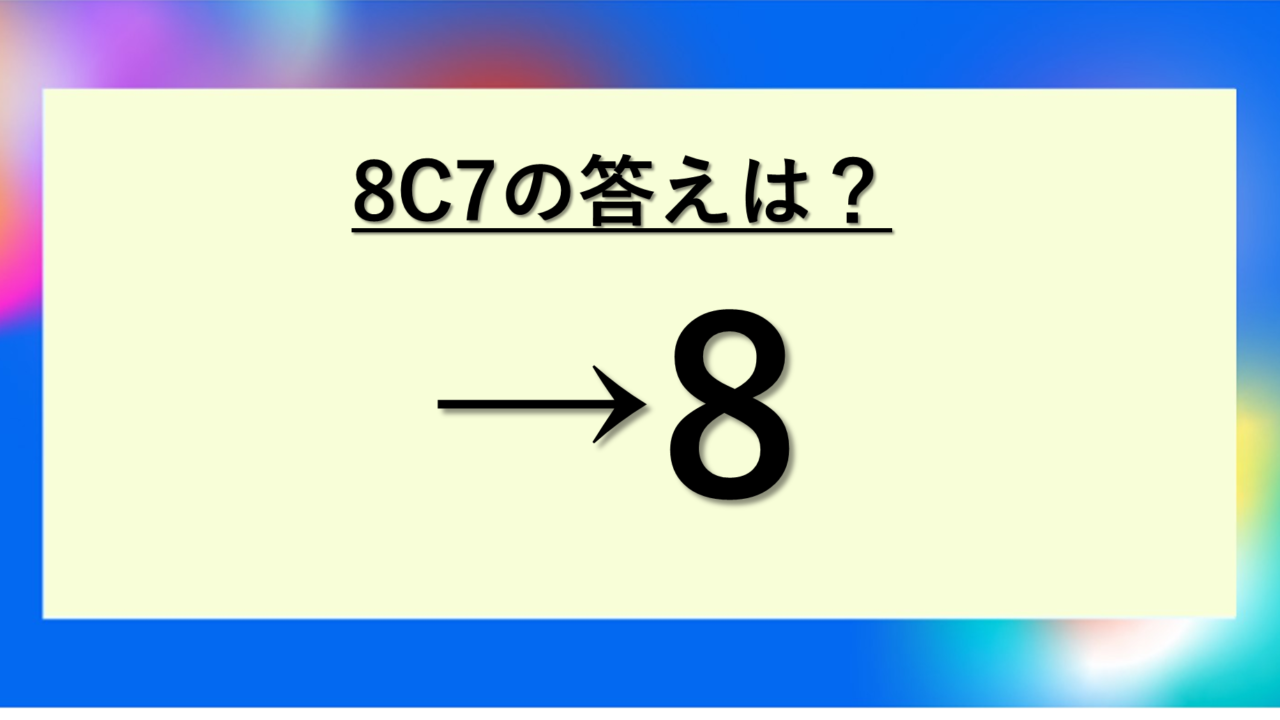
8C7の答えとその数学的な意味
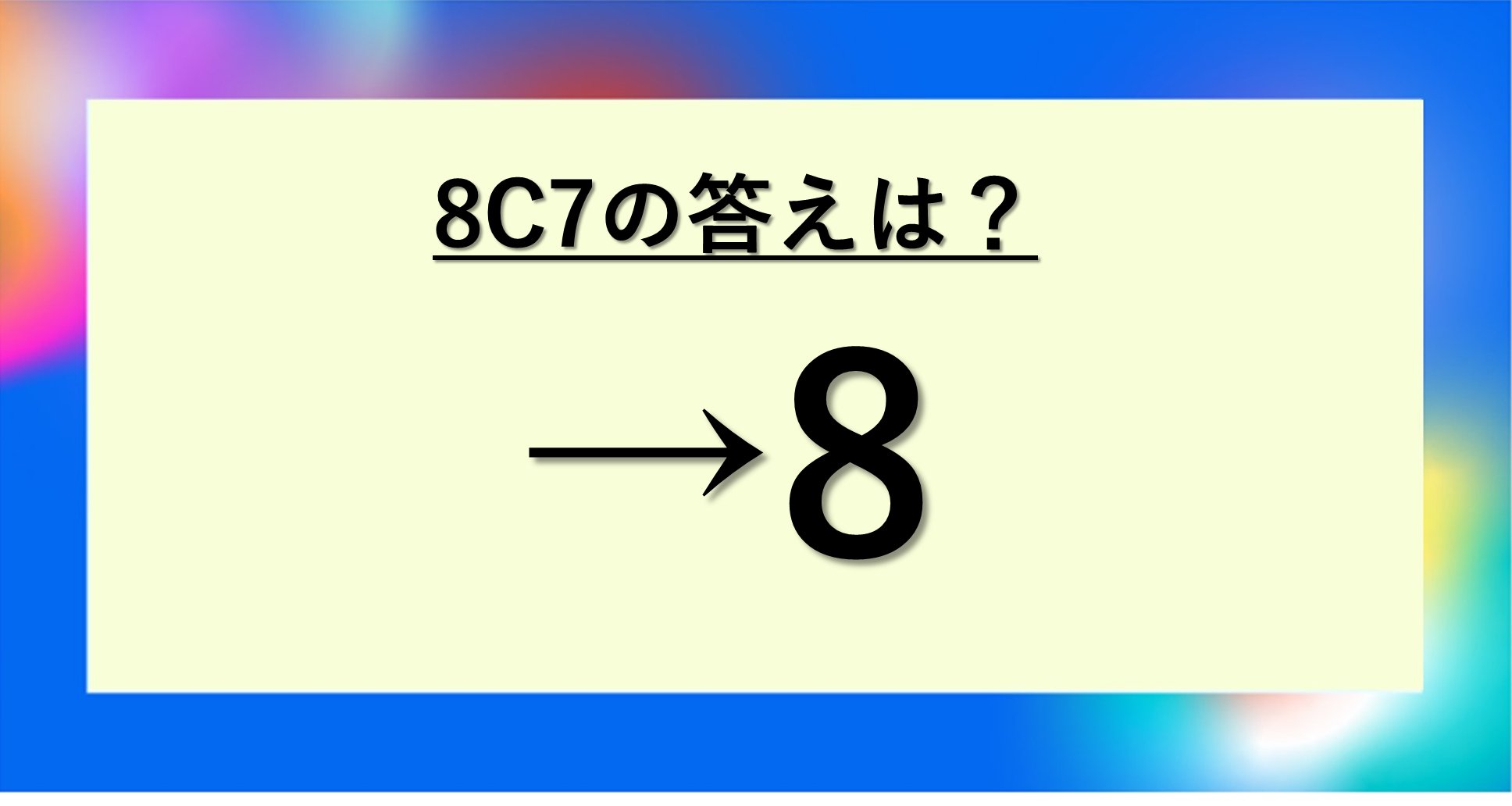
この答えは、8個のものから7個を選ぶ組み合わせの総数を表しています。意外とシンプルな数字に驚かれる方もいるかもしれませんね。
8個から7個を選ぶということは、逆に考えると「8個から1個だけを選ばない(残す)」ということになります。この視点の転換が、計算を理解する上で非常に重要なポイントになるでしょう。
組み合わせ記号の基本的な読み方
8C7という記号は、「8個の中から7個を選ぶ組み合わせの数」を表す数学的表記法です。
一般形としてはnCrと書かれ、nが全体の個数、rが選び取る個数を意味します。「C」は英語の「Combination(組み合わせ)」に由来しており、順序を考慮しない選び方を表すのです。
読み方は「8シー7」または「8コンビネーション7」となります。数学の授業や参考書では、前者の読み方が一般的に使われていますね。
8C7が表す実際の状況
8C7は日常生活のさまざまな場面で応用できる考え方になります。
例えば、8人のメンバーから7人を選んで旅行に行く場合の選び方が8C7です。また、8種類の食材から7種類を使って料理を作る際の組み合わせ数も同様に8C7で表現できます。
このような状況では、「誰を選ぶか」ではなく「誰を残すか」という視点で考えた方が分かりやすいケースが多いでしょう。8人から7人を選ぶということは、実質的に1人を選んで残すということと同じ意味を持つのです。
8C7の計算方法と求め方
続いては8C7の具体的な計算方法を確認していきます。
組み合わせの基本公式を使った計算
組み合わせの計算では、次の基本公式を使用します。
8C7 = 8! / (7! × 1!)
ここで「!」は階乗(ファクトリアル)を表す記号です。階乗とは、その数から1まで順番に掛け算していく計算方法を意味します。
例えば8! = 8×7×6×5×4×3×2×1となりますが、実際の計算ではすべてを展開する必要はありません。効率的な約分のテクニックを使えば、驚くほど簡単に計算できるのです。
実際の計算プロセス
8C7を効率的に計算する手順を見ていきましょう。
= (8 × 7!) / (7! × 1)
= 8 / 1
= 8
この計算では、分子と分母に共通する7!を約分しています。7!という大きな数を実際に計算することなく、約分だけで答えを導き出せる点がポイントですね。
分母の1!は1となり、分子には8だけが残ります。最後に8÷1を計算して答えの8が得られるわけです。非常にシンプルな計算で済むことが分かるでしょう。
計算の注意点とポイント
8C7のような組み合わせ計算で押さえておくべきポイントを整理します。
| 計算のステップ | 内容 | 8C7での具体例 |
|---|---|---|
| 公式の確認 | n! / (r! × (n-r)!) | 8! / (7! × 1!) |
| 約分の実行 | 共通の階乗を消去 | 7!を約分 |
| 残った計算 | 簡単な割り算 | 8 / 1 = 8 |
特に重要なのは、階乗を展開する前に約分できる部分を見つけることです。8!を全部展開してから計算しようとすると、40320という大きな数を扱うことになり、計算ミスの原因にもなりかねません。
効率的な計算方法を身につければ、テストや入試でも時間を節約できるようになるでしょう。
8C7と8C1が同じ値になる理由
続いては8C7と8C1の関係性について確認していきます。
補集合による対称性の原理
実は、8C7と8C1はどちらも答えが8で完全に一致します。これは偶然ではなく、組み合わせの持つ本質的な性質なのです。
nCr = nC(n-r)8C7 = 8C(8-7) = 8C1 = 8
この性質が成り立つ理由は、「8個から7個を選ぶ」ことと「8個から1個を選んで残す(選ばない)」ことが、実質的に同じ操作だからです。
7個を選ぶということは、裏を返せば1個を除外するということ。この視点の転換により、選ぶ数が多い問題を選ばない数で考えることができるようになります。
8C1の計算で検証
8C1を実際に計算して、本当に8になるか確認してみましょう。
= (8 × 7!) / (1 × 7!)
= 8 / 1
= 8
計算過程を見ると、8C7とまったく同じ形になることが分かります。分子には8が残り、分母は1となる点も完全に一致していますね。
また、8C1は「8個から1個を選ぶ方法の数」を意味するため、直感的にも8通りであることが理解できるでしょう。8個のものがあれば、そのうちどれか1つを選ぶ方法は確かに8通りあるのです。
対称性を活用した計算戦略
組み合わせの対称性を理解すると、計算効率が格段に向上します。
一般的な戦略として、rとn-rを比較して小さい方の数で計算すると楽になります。8C7の場合、7よりも1の方が小さいため、8C1として計算した方が圧倒的に簡単です。
| 元の組み合わせ | 変換後 | どちらが簡単か |
|---|---|---|
| 10C9 | 10C1 | 10C1の方が簡単 |
| 12C11 | 12C1 | 12C1の方が簡単 |
| 100C99 | 100C1 | 100C1の方が圧倒的に簡単 |
特にnとrの差が1の場合、つまりnCnやnC(n-1)のような形では、この性質を使うと瞬時に答えが分かるようになるでしょう。nC(n-1) = nC1 = nという関係を覚えておくと便利ですね。
組み合わせ計算の覚え方とコツ
続いては組み合わせ計算をマスターするためのコツを確認していきます。
公式の本質的な理解と記憶法
組み合わせの公式を単純に暗記するのではなく、意味を理解しながら覚えることが重要になります。
nCr = n! / (r! × (n-r)!) という公式の背景には、次のような考え方があります。まず、n個のものを1列に並べる方法はn!通り存在します。しかし組み合わせでは順序を考慮しないため、選んだr個の内部での並び替え(r!通り)と、選ばなかったn-r個の内部での並び替え((n-r)!通り)を除外する必要があるのです。
この理屈を理解すれば、公式を忘れても自分で導き出せる力が身につくでしょう。
よく出るパターンの暗記
組み合わせ計算には、覚えておくと便利な特殊なパターンがいくつか存在します。
– nC1 = n (1個選ぶ方法はn通り)
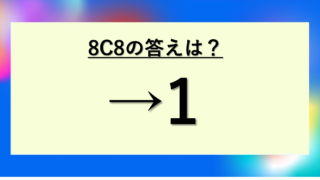
– nCn = 1 (全部選ぶ方法は1通り)
– nC(n-1) = n (n-1個選ぶ=1個残す方法はn通り)
これらのパターンを覚えておけば、8C7のような問題を見たときに即座に「8C1と同じだから答えは8」と判断できるようになります。
特にnC1とnC(n-1)の関係は頻出するため、セットで記憶しておくと効果的でしょう。テストや入試では計算時間の短縮につながりますね。
順列(P)との違いを明確に区別
組み合わせ(C)と順列(P)の違いを正確に理解することが、問題を解く上で極めて重要です。
| 比較項目 | 組み合わせ(C) | 順列(P) |
|---|---|---|
| 順序の考慮 | 考慮しない | 考慮する |
| 8個から7個選ぶ | 8C7 = 8通り | 8P7 = 40320通り |
| 適用場面 | チームメンバーを選ぶ | 役職を割り当てる |
| 公式 | n!/(r!(n-r)!) | n!/(n-r)! |
問題文に「選ぶ」「取り出す」とあれば組み合わせ、「並べる」「配置する」「順番に」とあれば順列を使います。役職や順序が関係するかどうかが判断の基準になるでしょう。
8P7を計算すると40320通りという膨大な数になり、8C7の8通りとは大きく異なります。この違いを正確に把握することで、問題の本質を見抜く力が養われますね。
8C7に関連する応用問題と考え方
続いては8C7を題材にした応用的な考え方を確認していきます。
確率問題への応用
8C7は確率計算の場面でも頻繁に登場します。
例えば、8個の製品があり、そのうち1個だけが不良品である場合を考えてみましょう。7個を選んだときに全て良品である確率を求める際、良品7個を選ぶ組み合わせが8C7に関連してきます。
8個の製品(良品7個、不良品1個)から7個を選ぶとき全て良品である選び方 = 7C7 = 1通り
7個を選ぶ全ての方法 = 8C7 = 8通り確率 = 1/8
このように、組み合わせの考え方は確率の分母や分子を求める際に不可欠なツールとなるのです。
場合の数との関連性
8C7は場合の数を数え上げる問題でも重要な役割を果たします。
8人の生徒から7人の代表を選ぶ方法、8冊の本から7冊を購入する方法など、様々な場面で8C7が活用できるでしょう。重要なのは、「選ぶ」という行為の裏側には必ず「選ばない」という行為が存在することです。
8個から7個選ぶ = 8個から1個除外するという等価な見方ができると、問題を多角的に捉えられるようになります。この視点の転換こそが、組み合わせ計算の本質を理解する鍵となるのです。
大きな数での計算への応用
8C7で学んだ対称性の原理は、もっと大きな数の組み合わせでも威力を発揮します。
例えば100C99を計算する場合、公式通りに計算しようとすると非常に複雑になります。しかし、100C99 = 100C1 = 100という関係を使えば、瞬時に答えが分かるでしょう。
| 問題 | 直接計算 | 対称性利用 | 答え |
|---|---|---|---|
| 50C49 | 複雑 | 50C1 | 50 |
| 200C199 | 非常に複雑 | 200C1 | 200 |
| 1000C999 | 計算不可能レベル | 1000C1 | 1000 |
このように、nとrの差が小さい場合は対称性を積極的に活用することで、計算が劇的に簡単になります。8C7で学んだ考え方は、あらゆる組み合わせ計算の基礎となるのです。
まとめ
8C7の計算方法と答えについて詳しく解説してきました。
8C7の答えは8であり、これは8個のものから7個を選ぶ組み合わせの総数を表します。計算には基本公式nCr = n! / (r! × (n-r)!)を使用しますが、効率的に約分することで非常にシンプルに答えを導き出せるのです。
特に重要なポイントは、8C7と8C1が同じ値になるという対称性でしょう。8個から7個を選ぶことは、8個から1個を選んで残すことと等価であり、この視点の転換が組み合わせ計算を理解する鍵となります。
組み合わせの計算は、確率や場合の数を求める際の基礎となる重要なスキルです。公式の意味を本質的に理解し、約分のテクニックや対称性の活用といった効率的な計算方法を身につければ、より複雑な問題にも自信を持って取り組めるようになるでしょう。
この記事で紹介した計算方法やコツを実践することで、8C7のような組み合わせ計算を素早く正確にこなせるはずです。数学の問題に対する理解を深め、実力アップにつなげていきましょう。