数学の組み合わせ計算で「12C4」という表記を見たとき、どのように計算すればよいのでしょうか。
12個のものから4個を選ぶという状況は、確率や場合の数の問題で頻繁に登場します。4個選ぶ組み合わせは計算がやや複雑に見えるかもしれませんが、対称性を活用すれば効率的に答えを導き出せるのです。
本記事では12C4の計算方法から答え、そしてなぜ12C8と同じ値になるのかという理由まで、丁寧に解説していきます。組み合わせの対称性を活用した効率的な計算方法や約分のコツもお伝えしますので、数学に苦手意識がある方でも安心して読み進めてください。
12C4の答えは495【結論と計算方法】
それではまず12C4の答えと計算方法について解説していきます。
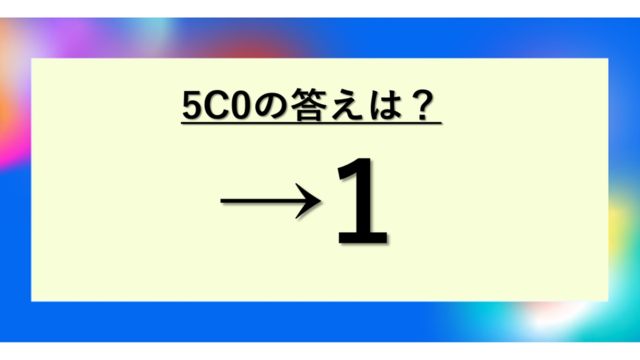
12C4の答えは495になる
12個のものから4個を選ぶ組み合わせの数は495通りということになります。この答えは組み合わせの公式を使って導き出せますが、計算の過程で約分を効率的に行うことが重要なポイントです。
また対称性を利用すれば、12C4=12C8という関係も成り立ちます。実際に計算する際は、4個選ぶ方が8個選ぶよりも圧倒的に簡単なので、必ず小さい方で計算しましょう。
組み合わせの公式を使った計算
組み合わせnCrの基本公式を使って計算してみましょう。
この公式に12C4を当てはめます。
= 12! / (4! × 8!)
= (12 × 11 × 10 × 9 × 8!) / (4 × 3 × 2 × 1 × 8!)
= (12 × 11 × 10 × 9) / (4 × 3 × 2 × 1)
= 11880 / 24
= 495
8!が分子と分母で約分されるため、実際には12×11×10×9を4×3×2×1で割る計算になります。
効率的な約分方法
計算をさらに効率化するため、約分しながら進める方法を紹介します。
12を4で割ると
= (3 × 11 × 10 × 9) / (1 × 3 × 2 × 1)
3同士で約分すると
= (1 × 11 × 10 × 9) / (1 × 1 × 2 × 1)
10を2で割ると
= (11 × 5 × 9) / 1
= 11 × 5 × 9
= 55 × 9
= 495
このように段階的に約分していけば、最後は掛け算だけになります。大きな数を割り算する必要がなくなるため、計算ミスも減るでしょう。
12C4=12C8となる理由【対称性の解説】
続いては12C4と12C8が同じ値になる理由を確認していきます。
選ぶことと残すことの対称性
組み合わせには重要な対称性があります。
この性質により、12C4=12C(12-4)=12C8が成立するのです。
12個のものから4個を選ぶという行為は、見方を変えれば12個のものから8個を選ばない(残す)という行為と完全に同じです。
例えば12枚のカードから4枚選ぶとき、選んだ4枚が決まれば、残った8枚も自動的に決まります。逆に、残す8枚を先に決めれば、選ぶ4枚も自動的に決まるでしょう。つまり「4枚選ぶ方法の数」と「8枚残す方法の数」は完全に一致するのです。
具体例で理解する一対一対応
小さな数字で具体的に考えてみましょう。
選ぶ4個 → 残る2個
ABCD → EF
ABCE → DF
ABCF → DE
ABDE → CF
ABDF → CE
ABEF → CD
…
6C4 = 6C2 = 15通り
このように、選ぶ組み合わせと残る組み合わせは一対一に対応しています。
| 計算 | 意味 | 答え |
|---|---|---|
| 8C4 | 8個から4個選ぶ | 70 |
| 8C4 | 8個から4個残す | 70 |
| 10C4 | 10個から4個選ぶ | 210 |
| 10C6 | 10個から6個残す | 210 |
| 12C4 | 12個から4個選ぶ | 495 |
| 12C8 | 12個から8個残す | 495 |
どの場合でも対称性が成り立っていることが分かります。
数式で証明する対称性
対称性を数式で証明してみましょう。
= (12 × 11 × 10 × 9) / (4 × 3 × 2 × 1)
= 11880 / 24
= 495
12C8 = 12! / (8! × 4!)
= (12 × 11 × 10 × 9) / (4 × 3 × 2 × 1)
= 11880 / 24
= 495
よって 12C4 = 12C8
分母の4!と8!の順序が入れ替わっているだけで、掛け算なので結果は同じになります。分子も分母も完全に一致するため、当然答えも同じになるのです。
組み合わせ計算のコツと覚え方
続いては組み合わせの計算を効率的に行うコツを確認していきます。
小さい方の数で計算する鉄則
組み合わせを計算する際の最も重要なコツは、rとn-rのうち小さい方を使うことです。
直接計算すると
12C8 = (12×11×10×9×8×7×6×5) / (8×7×6×5×4×3×2×1)
→ 分子も分母も8項ずつで非常に複雑
対称性を使うと
12C8 = 12C4 = (12×11×10×9) / (4×3×2×1) = 495
→ 分子4項、分母4項で圧倒的に簡単
常にrとn-rを比較して小さい方を選ぶ習慣をつけましょう。これにより計算量が劇的に減り、ミスも防げます。
約分を先に行う技術
階乗を展開してから約分するのではなく、計算しながら約分すると効率的です。
ステップ1:12と4を約分
(12÷4) × 11 × 10 × 9 / (3 × 2 × 1)
= 3 × 11 × 10 × 9 / (3 × 2 × 1)
ステップ2:3同士を約分
= 11 × 10 × 9 / (2 × 1)
ステップ3:10と2を約分
= 11 × 5 × 9
最終結果:11 × 5 × 9 = 495
このように、計算の途中で約分できる部分を見つけると、最後は簡単な掛け算だけになります。
階乗の部分約分テクニック
4!を展開せずに部分的に約分する方法もあります。
4! = 24と覚えておく
12C4 = (12 × 11 × 10 × 9) / 24
分子を先に計算:12 × 11 = 132
132 × 10 = 1320
1320 × 9 = 11880
11880 ÷ 24 = 495
4!=24という値を覚えておけば、計算がスムーズになります。よく使う階乗の値(3!=6、4!=24、5!=120)は暗記しておくと便利でしょう。
12C4を含む実践問題
続いては12C4が実際にどのような場面で使われるのかを確認していきます。
チーム編成問題での応用
12C4はチーム編成や選抜の問題でよく登場します。
解答:12C4 = 495通り
この問題は組み合わせの典型例です。12人のうちどの4人を選ぶかという問題なので、順序は関係なく組み合わせとして計算します。
もし「リーダー、副リーダー、会計、書記の4役を選ぶ」という問題であれば、役割が異なるため順列(12P4)になります。問題文をよく読んで、組み合わせか順列かを判断することが重要です。
トランプのポーカー問題
トランプゲームの確率計算でも12C4が使われることがあります。
解答:12C4 = 495通り
問題:1から12までの番号が書かれた12枚のカードから4枚を引いたとき、すべて偶数である確率は?
解答:
偶数は6個(2,4,6,8,10,12)
偶数から4枚選ぶ組み合わせ = 6C4 = 15通り
全体の組み合わせ = 12C4 = 495通り
確率 = 15/495 = 1/33
このように、全体の場合の数や特定条件を満たす場合の数を求める際に、組み合わせの計算が活用されます。
委員会選出の複合問題
複数の条件が組み合わさる問題でも使われます。
解答:
男子7人から2人選ぶ = 7C2 = 21通り
女子5人から2人選ぶ = 5C2 = 10通り
男女2人ずつの選び方 = 21 × 10 = 210通り
参考:全体の選び方 = 12C4 = 495通り
このように、条件付きの問題では複数の組み合わせを掛け合わせることがあります。全体の場合の数(12C4=495)と比較することで、確率を求めることもできるでしょう。
まとめ
12C4の計算方法と答えについて詳しく解説してきました。
12C4の答えは495であり、これは組み合わせの公式nCr=n!/(r!×(n-r)!)を使って計算できます。効率的に計算するには、約分を先に行いながら進めることが重要です。
12C4=12C8となる理由は、組み合わせの対称性nCr=nC(n-r)によるものでした。「12個から4個を選ぶこと」と「12個から8個を残すこと」は表裏一体の関係にあり、場合の数は完全に一致するのです。
計算の際は必ずrとn-rを比較して小さい方を使うこと、約分を途中で行うこと、4!=24などの基本的な階乗の値を覚えておくことがコツになります。これらのテクニックを使えば、大きな数の組み合わせでも素早く正確に計算できるでしょう。
12C4のような組み合わせは、チーム編成、カードゲーム、委員会選出など、実生活に関連する様々な場面で活用されます。基本をしっかり理解しながら、組み合わせの実用性と美しさを感じていただければ幸いです。