数学の組み合わせの計算で「4C0」という表記を見かけたとき、「0個選ぶってどういうこと?」と疑問に思った経験はありませんか。
確率や場合の数を学習していると、nCrという記号は頻繁に登場しますが、r=0のケース、つまり「1つも選ばない」という状況は直感的に理解しにくいものです。しかし、この4C0には明確な意味があり、組み合わせの理論において重要な役割を果たしています。
本記事では、4C0の計算方法や答えを詳しく解説するとともに、なぜその答えになるのかという理由や、覚え方のコツまで丁寧にお伝えしていきます。数学が苦手な方でも理解できるよう、具体例を交えながら説明していきますので、ぜひ最後までお読みください。
4C0の答えは1!その理由と数学的根拠
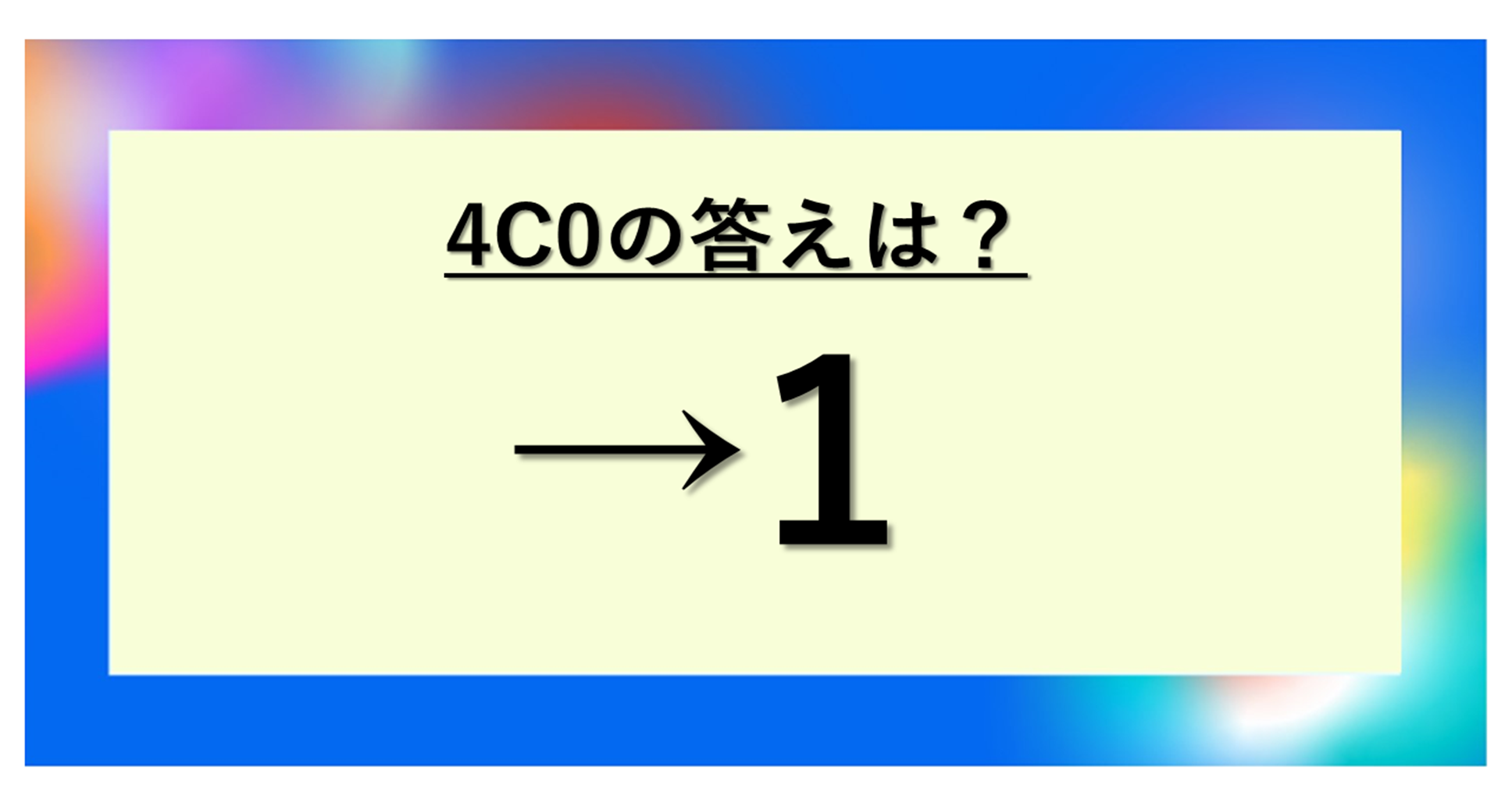
それではまず、4C0の答えとその理由について解説していきます。
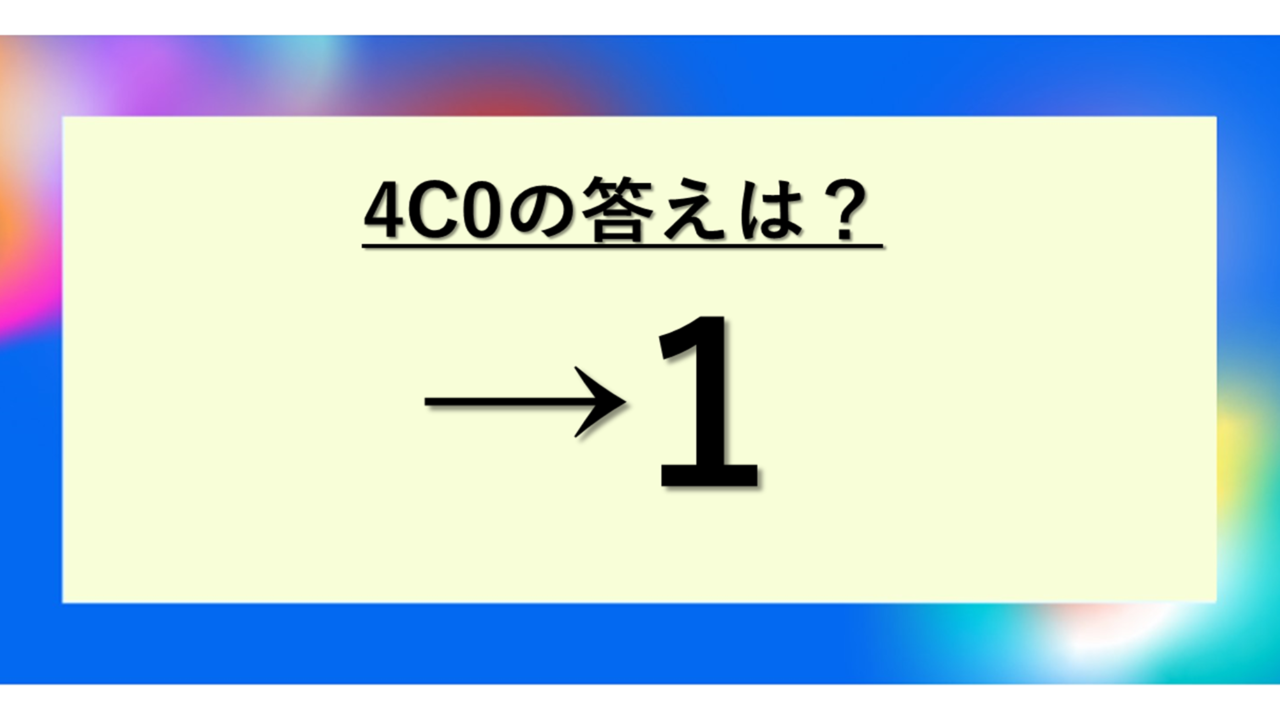
4C0 = 1
4個のものから0個選ぶ組み合わせの数は1通りです。
「何も選ばないのに1通り?」と不思議に感じるかもしれません。しかし、何も選ばないという選び方自体が1つの選択方法として成立しているのです。
たとえば、リンゴ、ミカン、バナナ、ブドウという4種類の果物があるとしましょう。この中から0個選ぶ場合、選び方は「何も選ばない」という1通りしかありません。2通りの「何も選ばない方法」は存在しないため、答えは1となります。
数学的には、組み合わせの公式を使っても同じ結果が得られます。組み合わせの公式は次のように表されます。
nCr = n! / (r! × (n-r)!)
この公式に n=4、r=0 を代入すると:
4C0 = 4! / (0! × 4!)
= 4! / (1 × 4!)
= 1
ここで重要なのは、0!(0の階乗)は1と定義されているという点です。この定義があるからこそ、組み合わせの公式が0個選ぶケースでも矛盾なく成立するのです。
なぜ0!は1なのか
0!が1である理由については、いくつかの説明方法があります。
最も分かりやすいのは「空集合の並べ方」という考え方でしょう。何もないものを並べる方法は1通り(何もしない)しかありません。また、階乗の定義から逆算して考えることもできます。
n! = n × (n-1)! という関係式があるため、1! = 1 × 0! となります。1! = 1 ですから、0! = 1 と定義することで数学的な整合性が保たれるわけです。
この定義は単なる約束事ではなく、組み合わせや順列の計算全体を矛盾なく成立させるための必然的な定義といえます。
実生活での4C0の意味
抽象的な数式だけでなく、実生活に当てはめて考えてみましょう。
たとえば、4つの選択肢があるアンケートで「該当するものをすべて選んでください(複数回答可)」という質問があったとします。この場合、「どれも該当しない」という回答は1通りの回答方法として成立します。
また、4種類のトッピングがあるアイスクリーム店で、「トッピングなし」を選ぶ方法は1通りです。トッピングなしのバニラアイスと、別のトッピングなしのバニラアイスは同じものですから、選び方は1通りということになります。
このように、「何も選ばない」という状態そのものが1つの明確な選択であることを理解すれば、4C0=1という答えに納得できるはずです。
組み合わせ全体における4C0の位置づけ
4個のものから選ぶ組み合わせをすべて列挙してみると、4C0の意味がさらに明確になります。
| 選ぶ個数 | 記号 | 組み合わせの数 |
|---|---|---|
| 0個選ぶ | 4C0 | 1通り |
| 1個選ぶ | 4C1 | 4通り |
| 2個選ぶ | 4C2 | 6通り |
| 3個選ぶ | 4C3 | 4通り |
| 4個選ぶ | 4C4 | 1通り |
興味深いのは、4C0と4C4が同じく1通りであることです。4個すべてを選ぶ方法も、何も選ばない方法も、それぞれ1通りしかありません。
また、これらをすべて足し合わせると 1+4+6+4+1=16 となり、これは2の4乗に等しくなります。このことからも、4C0=1という値が組み合わせの理論全体で整合性を持っていることが分かるでしょう。
4C0の計算方法を段階的に理解する
続いては、4C0の計算方法を確認していきます。
組み合わせの計算には複数のアプローチがありますが、ここでは最も基本的な公式を使った方法から、直感的な理解まで幅広く見ていきましょう。
組み合わせの公式を使った計算手順
組み合わせの基本公式を使った計算方法を、ステップごとに確認していきます。
ステップ1:公式に数値を代入
nCr = n! / (r! × (n-r)!)
n=4、r=0 を代入
4C0 = 4! / (0! × (4-0)!)
ステップ2:括弧内を計算
4C0 = 4! / (0! × 4!)
ステップ3:階乗を計算
4! = 4 × 3 × 2 × 1 = 24
0! = 1(定義)
4C0 = 24 / (1 × 24)
ステップ4:分母を計算
4C0 = 24 / 24 = 1
この計算過程で最も重要なポイントは、やはり0!を1として扱うことです。この約束を知っていれば、どんなnC0でも必ず答えは1になることが分かります。
実際、5C0でも100C0でも、同じ理屈で答えは1になります。n! が分子と分母で約分されるため、結果は常に 1/1 = 1 となるのです。
簡略化された計算方法
毎回公式を使って計算するのは面倒だという方には、簡略化された考え方があります。
組み合わせの公式は、次のようにも書き換えられます。
nCr = n × (n-1) × … × (n-r+1) / r!
4C0の場合、r=0なので:
分子:掛け算する数が0個(何も掛けない)= 1
分母:0! = 1
よって 4C0 = 1/1 = 1
この方法では、「r個の数を掛ける」という操作において、0個掛けるということは「何も掛けない」つまり1を意味します。これも「何もしない」という操作が明確に定義されている数学の美しさといえるでしょう。
パスカルの三角形を使った理解
パスカルの三角形を使うと、4C0の値を視覚的に理解できます。
| 1 | ||||
| 1 | 1 | |||
| 1 | 2 | 1 | ||
| 1 | 3 | 3 | 1 | |
| 1 | 4 | 6 | 4 | 1 |
最下段が4個のものから選ぶ組み合わせを表しており、左端の1が4C0に相当します。パスカルの三角形では、どの行も両端は必ず1になるという規則性があり、これがnC0=1とnCn=1を示しています。
パスカルの三角形の各数は、その上の2つの数の和として求められます。この性質を使えば、計算式を使わなくても組み合わせの数を視覚的に導き出せるのです。
組み合わせの基礎知識と関連する概念
続いては、組み合わせの基礎知識と関連概念を確認していきます。
4C0をより深く理解するには、組み合わせ全般についての知識が役立ちます。ここでは、組み合わせと順列の違いや、実際の応用例などを見ていきましょう。
組み合わせと順列の違い
組み合わせ(Combination)と順列(Permutation)は混同しやすい概念ですが、明確な違いがあります。
組み合わせは「選ぶだけ」で順序を考えないのに対し、順列は「選んで並べる」ため順序まで考慮します。
組み合わせの例:
A、B、Cの3人から2人を選ぶ
→ AB、AC、BC の3通り
(ABとBAは同じ組み合わせ)
順列の例:
A、B、Cの3人から2人を選んで並べる
→ AB、BA、AC、CA、BC、CB の6通り
(ABとBAは別の順列)
4C0の場合、順列で考えると4P0となりますが、これも答えは1です。0個のものを並べる方法は1通り(何もしない)しかありません。
nC0とnP0はどちらも必ず1になるという共通点がありますが、r≧1の場合は nPr ≧ nCr という関係になります。これは、同じものを選んでも並べ方が複数あるためです。
二項定理との関係
組み合わせの数は、二項定理と密接に関係しています。
二項定理とは、(a+b)ⁿ を展開したときの係数が組み合わせの数になるという定理です。
(a+b)⁴ を展開すると:
= 4C0×a⁴b⁰ + 4C1×a³b¹ + 4C2×a²b² + 4C3×a¹b³ + 4C4×a⁰b⁴
= 1×a⁴ + 4×a³b + 6×a²b² + 4×ab³ + 1×b⁴
ここで、最初の項の係数が4C0=1であることが分かります。これは数学的な美しい対称性を示しており、組み合わせの理論が代数学の様々な分野で活用されていることを物語っています。
また、a=b=1を代入すると、(1+1)⁴=2⁴=16 となり、これは先ほど見た4C0+4C1+4C2+4C3+4C4の合計と一致します。
実際の場面での応用例
組み合わせの考え方は、日常生活や様々な分野で活用されています。
確率の計算では、組み合わせが頻繁に使われます。たとえば、52枚のトランプから5枚を引く方法は52C5通りあり、これがポーカーの手札の総数になります。
また、宝くじの当選確率を計算する際にも組み合わせが使われます。ロト6では43個の数字から6個を選ぶため、43C6=6,096,454通りの組み合わせがあり、1等が当たる確率は約1/610万となります。
ビジネスの場面でも、プロジェクトチームの編成や商品の組み合わせ販売など、組み合わせの考え方が役立ちます。10人の候補者から3人のチームを作る方法は10C3=120通りあり、すべての可能性を検討する際の基準となるでしょう。
さらに、情報科学の分野では、暗号理論やアルゴリズムの計算量評価などで組み合わせ論が重要な役割を果たしています。
4C0を含む組み合わせの覚え方とコツ
続いては、4C0を含む組み合わせの覚え方とコツを確認していきます。
組み合わせの計算は公式を覚えるだけでなく、いくつかのパターンや性質を理解しておくと、より素早く正確に解けるようになります。
nC0とnCnは必ず1というルール
組み合わせの計算で最初に覚えるべきルールは、nC0=1とnCn=1は常に成立するということです。
覚えておくべき基本ルール
・nC0 = 1(何も選ばない方法は1通り)
・nCn = 1(すべて選ぶ方法は1通り)
・nC1 = n(1個選ぶ方法はn通り)
・nC(n-1) = n(n-1個選ぶ=1個残す方法はn通り)
これらの規則を知っていれば、計算しなくても瞬時に答えが分かる問題が増えます。
たとえば、100C0も1000C0も答えは1です。また、5C5=1、20C20=1というように、nがどんな数でもnCn=1となります。
さらに、nCrとnC(n-r)は等しいという対称性もあります。4C1=4C3=4、4C2=6というように、選ぶ個数と選ばない個数が同じなら組み合わせの数も同じになるのです。
小さい数から順に計算する練習法
組み合わせの感覚を身につけるには、小さい数から順に計算してパターンを掴むのが効果的です。
| n | nC0 | nC1 | nC2 | nC3 | 合計 |
|---|---|---|---|---|---|
| 0 | 1 | – | – | – | 1 |
| 1 | 1 | 1 | – | – | 2 |
| 2 | 1 | 2 | 1 | – | 4 |
| 3 | 1 | 3 | 3 | 1 | 8 |
| 4 | 1 | 4 | 6 | 4 | 16 |
この表を見ると、いくつかの規則性が見えてきます。
まず、各行の左端(nC0)は必ず1です。次に、合計列を見ると1、2、4、8、16と2のべき乗になっています。これは2ⁿという規則性です。
また、各行は左右対称になっています。3C0=3C3=1、3C1=3C2=3というように、選ぶ個数が反対でも答えは同じなのです。
このような表を自分で作ってみることで、組み合わせの数がどのように変化するのか、直感的に理解できるようになります。
つまずきやすいポイントと対策
組み合わせの学習でつまずきやすいポイントをいくつか紹介します。
最も多い間違いは、0!を0だと思い込んでしまうことです。0!=1という定義は直感に反するように感じられるかもしれませんが、これは数学的な整合性のために必要な約束事です。この点をしっかり理解しましょう。
次に多いのが、組み合わせと順列を混同してしまうケースです。「選ぶだけ」なのか「選んで並べる」のかを常に意識することが大切です。問題文に「順番は関係ない」「並べる」などのキーワードがあれば、それがヒントになります。
また、計算ミスを防ぐには、答えが妥当かどうかを確認する習慣をつけましょう。たとえば、nCrの答えがnより大きくなることはありません(nC1=nが最大)。もし計算結果がnを超えたら、どこかで間違えている可能性が高いでしょう。
チェックポイント
・nCr ≦ nPr(組み合わせは順列以下)
・nCr = nC(n-r)(対称性の確認)
・nC0 = nCn = 1(両端は1)
これらのチェックポイントを使って、自分の答えが正しいかどうか検証する癖をつけると、正答率が大きく向上します。
まとめ
4C0の計算方法と答えについて詳しく解説してきました。
4C0の答えは1であり、これは「何も選ばない」という選択自体が1通りの方法として成立することを意味しています。公式nCr=n!/(r!×(n-r)!)に当てはめると、0!=1という定義によって4C0=1が導かれます。
組み合わせの計算では、nC0=1、nCn=1という基本ルールや、nCr=nC(n-r)という対称性を理解しておくことが重要です。また、パスカルの三角形や二項定理との関係を知ることで、より深い理解が得られるでしょう。
つまずきやすいポイントとしては、0!の定義や組み合わせと順列の違いがありますが、小さい数から順に計算して規則性を掴むことで、自然と理解が深まっていきます。
数学の組み合わせは、確率計算や日常生活の様々な場面で応用される実用的な知識です。4C0=1という一見不思議な答えも、理論全体の整合性を保つための重要な要素となっています。本記事の内容を参考に、組み合わせの理解を深めていただければ幸いです。