組み合わせの計算において、10C6は実践的な問題で頻繁に登場する重要な計算です。「10個から6個を選ぶ組み合わせ」という設定は、確率問題や場合の数の問題でよく見られるパターン。
「10C6の計算方法が分からない」「答えはどうやって求めるの?」「10C4と同じ値になるって聞いたけど、なぜ?」こうした疑問を持つ方は多いでしょう。6個も選ぶとなると、計算が複雑に見えるかもしれません。
しかし実は、対称性を使えば計算が驚くほど簡単になります。10C6は10C4と等しく、4個選ぶ計算に置き換えられるのです。この性質を理解すれば、計算の効率が格段に上がるでしょう。
本記事では、10C6の計算方法と答えを基礎から丁寧に解説します。組み合わせの公式の使い方、10C4との対称性、効率的な計算テクニック、そして実践的な覚え方まで、確率・場合の数を完全にマスターするための情報を網羅的にお届けしますので、ぜひ最後までご覧ください。
10C6とは?6個選ぶ組み合わせの意味
それではまず、10C6が何を表しているのかについて解説していきます。
10C6が表す具体的な状況
10C6は「10個の異なるものの中から6個を選ぶ組み合わせの総数」を意味します。ここで重要なのは、選ぶ順番は考慮しないという点です。
日常生活や試験問題でよく見られる具体例を見てみましょう。
・10人のクラスから6人の代表を選ぶ
・10種類の科目から6科目を受講する
・10枚のカードから6枚を選ぶ
・10個の商品から6個を購入する
・10人のチームから6人を試合に出す
いずれの場合も、「A、B、C、D、E、Fを選ぶ」ことと「F、E、D、C、B、Aを選ぶ」ことは同じ組み合わせとして扱います。順序は関係ないため、組み合わせ(C)を使用するのです。
10C6の特徴は、半分より多く選ぶという点。10個のうち6個を選ぶということは、4個を選ばないということでもあります。この「選ばない4個」に注目することが、計算を簡単にする鍵となるでしょう。
10C6と10C4の関係性
10C6を理解する上で最も重要なのが、10C4との関係です。実は、10C6 = 10C4という等式が成り立つのです。
| 視点 | 10C6 | 10C4 |
|---|---|---|
| 意味 | 10個から6個を選ぶ | 10個から4個を選ぶ |
| 別の視点 | 10個から4個を選ばない | 10個から6個を選ばない |
| 答え | 210 | 210 |
この関係が成り立つ理由は、対称性の法則によるもの。10個から6個を選ぶことは、同時に4個を選ばないことを意味します。逆に、4個を選ぶことは6個を選ばないことと同じ。
つまり、選ぶ6個と選ばない4個が一対一で対応するため、組み合わせの総数も等しくなるのです。この性質を知っていれば、10C6を計算する際に10C4として計算できるため、効率が大幅に向上するでしょう。
なぜ10C6を学ぶ必要があるのか
10C6は組み合わせの中でも、実践的で重要な計算です。その理由を整理してみましょう。
1. 対称性の理解を深める絶好の例
2. 計算効率化のテクニックを学べる
3. 確率問題で頻出のパターン
4. より大きな組み合わせ計算の基礎
特に重要なのは、対称性を活用した計算効率化です。10C6を直接計算すると分子が6個の掛け算になりますが、10C4に変換すれば4個の掛け算で済みます。この差は、より大きな数の組み合わせ(例:100C97など)で決定的に重要になるのです。
また、10C6=210という値は、10C4と同じく覚えておくと便利な数字。試験で頻出するため、計算方法とともに答えも記憶しておくとよいでしょう。
10C6の計算方法と答え
続いては、10C6の具体的な計算方法を確認していきます。
組み合わせの公式を使った直接計算
まず、10C6を公式に従って直接計算してみましょう。
nCr = n! / (r! × (n-r)!)10C6の場合:
n = 10、r = 6なので
10C6 = 10! / (6! × 4!)
階乗を展開してみましょう。
10! = 10 × 9 × 8 × 7 × 6 × 5 × 4 × 3 × 2 × 1
6! = 6 × 5 × 4 × 3 × 2 × 1 = 720
4! = 4 × 3 × 2 × 1 = 24
これを代入すると、6!が分子と分母で約分できます。
10C6 = (10 × 9 × 8 × 7 × 6!) / (6! × 24)
= (10 × 9 × 8 × 7) / 24
= 5,040 / 24
= 210
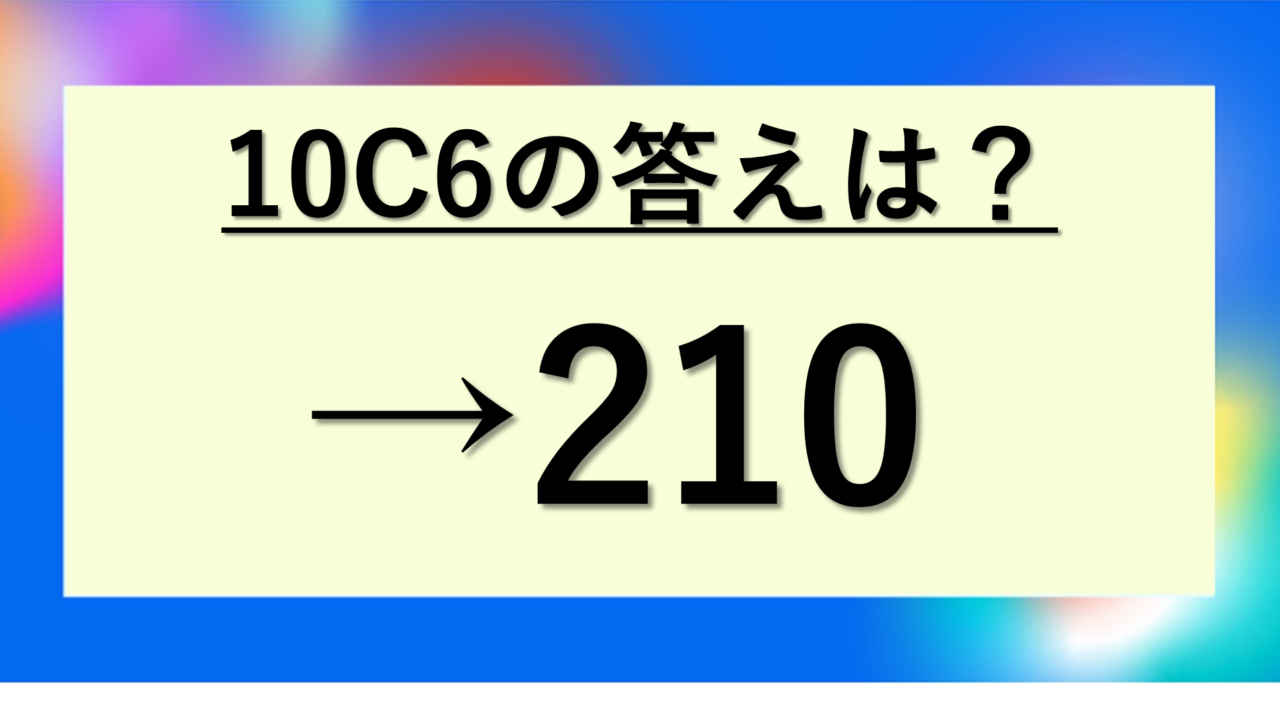
したがって、10C6の答えは210です。
対称性を活用した効率的な計算
実際の計算では、対称性を使った方法が圧倒的に効率的です。10C6 = 10C4という性質を使えば、計算が簡単になります。
対称性を使った計算10C6 = 10C(10-6) = 10C4に変換
10C4 = 10! / (4! × 6!)
= (10 × 9 × 8 × 7) / (4 × 3 × 2 × 1)
= (10 × 9 × 8 × 7) / 24
= 5,040 / 24
= 210
さらに効率を上げるため、途中で約分する方法もあります。
(10 × 9 × 8 × 7) / (4 × 3 × 2 × 1)
ここで約分:
・8と4で約分 → 2と1
・9と3で約分 → 3と1
すると:
(10 × 3 × 2 × 7) / (1 × 1 × 2 × 1)
= (10 × 3 × 2 × 7) / 2
= 10 × 3 × 7
= 210
| 計算方法 | 分子の掛け算 | 効率 |
|---|---|---|
| 10C6を直接計算 | 6個の掛け算 | 低い |
| 10C4に変換 | 4個の掛け算 | 高い |
| 途中で約分 | 3個の掛け算(10×3×7) | 最高 |
この約分テクニックを使えば、計算ミスを減らしながら素早く答えを出せます。試験では時間が限られているため、常に対称性を確認する習慣をつけましょう。
検算と答えの確認方法
計算ミスを防ぐため、答えが正しいか確認する方法を知っておきましょう。
10C6 = 210という答えが妥当かどうか、複数の角度からチェックできます。
3. 10C4 = 210と等しいはず(対称性) → 210 = 210 ✓
4. 10P6より小さいはず → 210 < 151,200 ✓
また、パスカルの三角形の性質を使った検算も可能です。10C6 = 9C6 + 9C5という関係があります。
9C6 = 84
9C5 = 126
84 + 126 = 210 ✓
確かに正しい答えであることが確認できました。ただし、基本的には対称性を使って10C4として計算するのが最も確実で効率的でしょう。
10C6=10C4となる理由と対称性の本質
続いては、なぜ10C6と10C4が等しくなるのか、その本質を確認していきます。
対称性の法則の数学的根拠
組み合わせには、nCr = nC(n-r)という重要な性質があります。これが対称性の法則です。
10の場合、以下のような対応関係が成り立ちます。
・10C0 = 10C10 = 1
・10C1 = 10C9 = 10
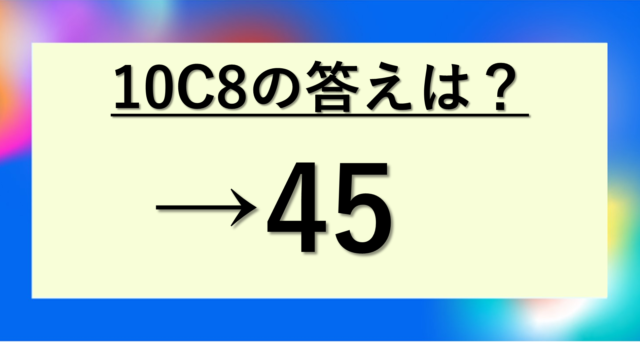
・10C2 = 10C8 = 45
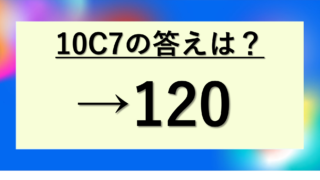
・10C3 = 10C7 = 120
・10C4 = 10C6 = 210
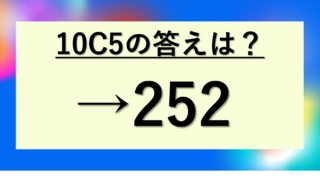
・10C5 = 10C5 = 252
この法則が成り立つ理由を、公式から確認してみましょう。
10C6 = 10! / (6! × (10-6)!)
= 10! / (6! × 4!)
10C4 = 10! / (4! × (10-4)!)
= 10! / (4! × 6!)
分母の6!と4!の順序が入れ替わっただけで、掛け算なので結果は同じ。つまり、10C6 = 10C4が数学的に証明されるのです。
6個選ぶことと4個選ばないことの対応
具体例で考えると、対称性の意味がより明確になるでしょう。A、B、C、D、E、F、G、H、I、Jの10人がいるとします。
| 10C6(6人を選ぶ) | 10C4(4人を選ぶ=6人を選ばない) |
|---|---|
| A、B、C、D、E、Fを選ぶ | G、H、I、Jを選ぶ(=A〜Fを選ばない) |
| A、B、C、D、G、Hを選ぶ | E、F、I、Jを選ぶ(=A、B、C、D、G、Hを選ばない) |
| E、F、G、H、I、Jを選ぶ | A、B、C、Dを選ぶ(=E〜Jを選ばない) |
10C6で「A、B、C、D、E、Fを選ぶ」という1つの組み合わせは、10C4で「G、H、I、Jを選ぶ」という1つの組み合わせと完全に一対一で対応しています。
選ぶ6人と選ばない4人(=選ぶ4人)が対応するため、組み合わせの総数も必ず等しくなるわけです。この美しい対称性は、組み合わせの本質的な性質と言えるでしょう。
対称性を活用した実践的テクニック
対称性の法則は、実際の問題を解く際に非常に強力な武器となります。特にrが大きい場合に活用すると効果絶大です。
対称性活用の鉄則原則:r > n/2 のとき、必ずnC(n-r)に変換
理由:
・計算量が減る
・ミスが減る
・時間が短縮される
例:
・10C6 → 10C4(6個→4個の掛け算に削減)
・50C48 → 50C2(48個→2個の掛け算に削減)
・100C97 → 100C3(97個→3個の掛け算に削減)
具体的な効果を見てみましょう。
分子:10×9×8×7×6×5(6個の掛け算)
分母:6! = 720(大きい)
計算の手間:大10C4に変換:
分子:10×9×8×7(4個の掛け算)
分母:4! = 24(小さい)
計算の手間:小
このように、対称性を知っているかどうかで、計算の難易度が劇的に変わるのです。試験では必ず活用すべき重要テクニックでしょう。
常にrとn-rを比較し、小さいほうで計算する習慣をつけることを強くおすすめします。この習慣は、より大きな組み合わせ計算でも役立ちます。
10C6の覚え方と実践的活用法
続いては、10C6を確実にマスターし実践で活用するためのポイントを確認していきます。
効率的な覚え方と記憶のコツ
10C6の覚え方で最も重要なのは、10C4と同じ値であることを覚えることです。
10C6 = 10C4 = 210計算方法:
10C4として計算
= (10 × 9 × 8 × 7) / 24
= 5,040 / 24
= 210
または約分して:
10 × 3 × 7 = 210
nC6の一般的なパターンも押さえておくとよいでしょう。
| 組み合わせ | 対称変換 | 答え |
|---|---|---|
| 6C6 | 6C0 | 1 |
| 10C6 | 10C4 | 210 |
| 20C6 | 20C14(変換しない方が楽) | 38,760 |
| 100C6 | 100C94 → 100C6のまま計算 | 1,192,052,400 |
注意点として、nC6の場合はrが小さいので、対称変換しない方が計算が楽なことが多いです。常にrとn-rを比較して、小さい方で計算しましょう。
実際の確率問題での応用例
10C6は、実際の確率・場合の数の問題でどのように使われるのでしょうか。典型的な問題を見てみましょう。
10人の生徒から6人の委員を選ぶとき、特定の2人(AさんとBさん)が両方とも選ばれる確率を求めよ。解答
全体の場合の数:10C6 = 210通り
AさんとBさんが両方選ばれる場合:
残り8人から4人を選ぶ → 8C4 = 70通り
確率:70/210 = 1/3
このように、全体の場合の数として10C6を使うパターンが非常に多いのです。
より実践的な例も見てみましょう。
1から10までの数字が書かれた10枚のカードから6枚を選ぶ。このとき、選んだ6枚にすべて含まれるのは何通りか。ただし、1と10は必ず含まれるものとする。解答
1と10は確定なので、残り8枚から4枚を選ぶ
8C4 = (8×7×6×5)/(4×3×2×1)
= 1,680/24
= 70通り(確認:全パターン10C6 = 210通り)
10C6単体だけでなく、条件を加えた応用問題も多いのです。基本をしっかり押さえておけば、こうした応用問題にも柔軟に対応できるでしょう。
よくある間違いと確実な対策
10C6の計算でよくある間違いとその対策をまとめました。
× 10×9×8×7×6×5 = 151,200…
○ 10C4に変換して計算ミス2:10C6と10P6を混同
10P6 = 151,200 ≠ 10C6 = 210
ミス3:分母の計算ミス
× 6! = 120と間違える
○ 6! = 720(または4! = 24で計算)
ミス4:約分のミス
○ 段階的に約分して確実に
これらのミスを防ぐには、必ず対称性をチェックすることが重要です。r > n/2なら、必ずnC(n-r)に変換してから計算しましょう。
また、10C6 = 10C4 = 210という関係を覚えておけば、計算ミスに気づきやすくなります。答えが210から大きく外れていたら、どこかで間違えているサインです。
まとめ
10C6の計算方法と答え、そして10C4との対称性について詳しく解説してきました。
10C6は「10個から6個を選ぶ組み合わせ」を表し、答えは210です。計算方法は、公式nCr = n!/(r!×(n-r)!)を使い、10C6 = 10!/(6!×4!) = (10×9×8×7)/24 = 210となります。しかし実際には、対称性の法則により10C6 = 10C4なので、10C4として計算するのが最も効率的です。
最も重要なポイントは、10C6 = 10C4という対称性。これは「6個を選ぶ」ことと「4個を選ぶ(=6個を選ばない)」ことが完全に対応しているためです。この性質を理解すれば、計算の効率が格段に上がります。6個の掛け算が4個の掛け算に減り、分母も720から24に小さくなるのです。
覚え方のコツとしては、10C6を見たら即座に10C4に変換する習慣をつけること。r > n/2のときは必ずnC(n-r)に変換するという原則を守れば、どんな組み合わせでも効率的に計算できます。また、10C6 = 210という答えも、10C4と同じ値であることとセットで記憶しておくとよいでしょう。
10C6は対称性を活用する絶好の例。ここで学んだ計算効率化のテクニックは、より大きな組み合わせ計算でも威力を発揮します。確実にマスターして、確率・場合の数の問題を自信を持って解けるようになりましょう。