組み合わせの計算で「8C8」という表記を見たとき、どう考えればよいのか戸惑う方もいるかもしれません。
8個のものから8個すべてを選ぶ組み合わせを表す8C8は、直感的に考えれば答えが分かる特殊なケースです。しかし、なぜその答えになるのか、公式を使ってどう計算するのかを理解することで、組み合わせの本質的な理解が深まります。
この記事では、8C8の具体的な計算方法から答えまでを丁寧に解説していきます。さらに、nCnという形の組み合わせが持つ特別な意味や、組み合わせ計算全般に使える覚え方のコツについても詳しく説明しますね。
確率や場合の数を求める際に必要不可欠な組み合わせの考え方。8C8という一見シンプルな問題を通じて、組み合わせの基礎から応用までをしっかりマスターしていきましょう。それでは早速、8C8の答えと基本的な意味から確認していきます。
8C8の答えは1!組み合わせの基本原理を理解しよう
それではまず、8C8の計算結果とその基本的な意味について解説していきます。
8C8の答えとその数学的な意味
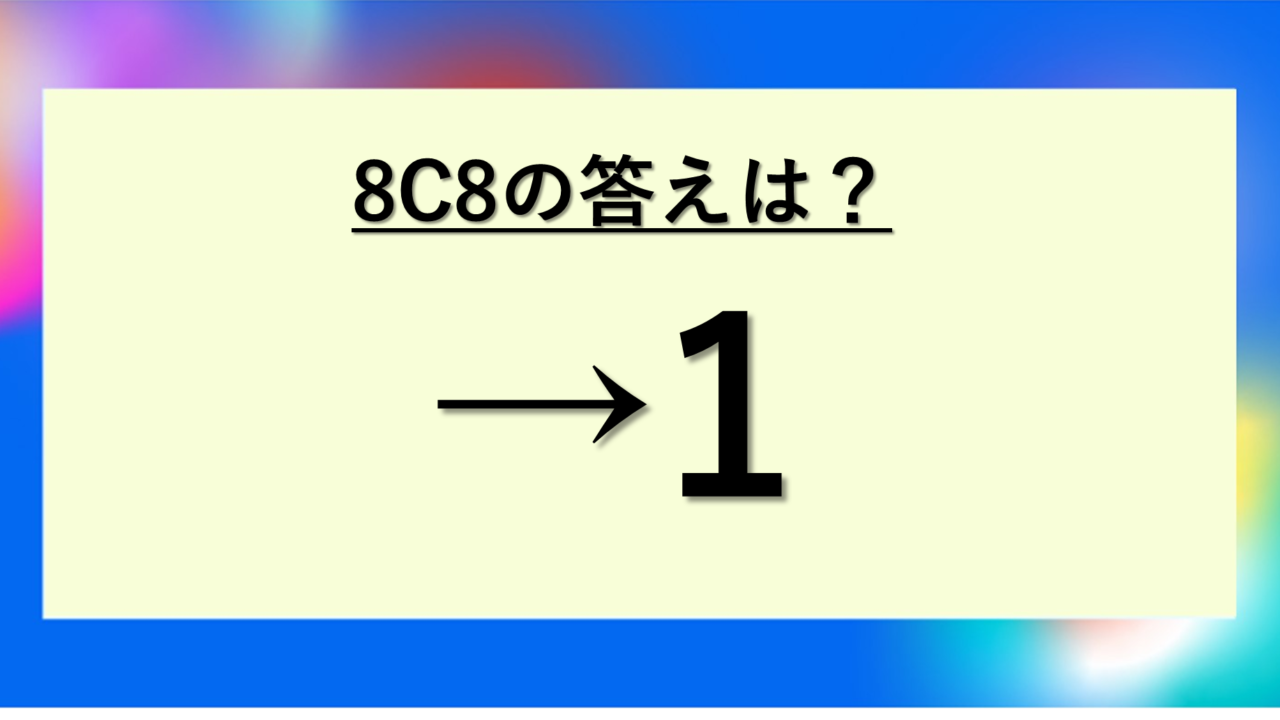
この答えは、8個のものから8個すべてを選ぶ組み合わせの総数を表しています。すべてを選ぶ方法は1通りしかないため、答えは1になるのです。
直感的に考えても理解しやすいでしょう。8個のものがあって、その8個全部を選ぶ場合、選び方は「全部選ぶ」という1つの方法しかありません。どれを先に選んでも最終的には全部選ぶことになるため、組み合わせとしては1通りなのです。
nCnという特殊な形の意味
8C8は、一般形で表すとnCnという形になります。これは「n個からn個すべてを選ぶ組み合わせ」を意味する特殊なケースです。
nCnの答えは、nがどんな数であっても常に1になります。5C5も10C10も100C100も、すべて答えは1です。これは組み合わせの持つ重要な性質の1つでしょう。
すべてを選ぶという行為には選択の余地がないため、どのような状況でも1通りしか存在しないのです。この理解は、組み合わせの基本的な考え方を身につける上で非常に重要になります。
8C8が表す実際の状況
8C8は日常生活でも様々な場面で登場する考え方です。
例えば、8人全員が参加する委員会を作る場合の作り方が8C8になります。また、8種類の材料をすべて使って料理を作る際の材料の選び方も8C8で表現できるでしょう。
このような状況では、「選ぶ」という行為はあっても、実質的には選択の自由がないことになります。すべてを選ぶと決まっているため、組み合わせとしては1通りしかないのです。
確率の問題でも、「すべてを選ぶ確率」を考える際に8C8が分母や分子に登場することがあります。この場合、8C8 = 1という値を理解していることが重要になるでしょう。
8C8の計算方法と求め方
続いては8C8の具体的な計算方法を確認していきます。
組み合わせの基本公式を適用
8C8も他の組み合わせと同様に、基本公式を使って計算できます。
8C8 = 8! / (8! × 0!)
ここで注目すべきは、n-rの部分が8-8=0となり、0!が登場する点です。0!の値は1と定義されています。これは数学的な約束事であり、組み合わせの計算を整合的にするための重要な定義なのです。
階乗の基本として、n! = n×(n-1)×…×2×1ですが、0!だけは特別に1と定められています。この定義により、nCnのような特殊なケースでも公式が正しく機能するわけですね。
実際の計算プロセス
8C8を公式に従って計算する手順を見ていきましょう。
= 8! / (8! × 1)
= 8! / 8!
= 1
この計算では、0! = 1を使って式を整理しています。分母の8!と分子の8!が約分されて、最終的に1だけが残るのです。
分子と分母に同じ階乗が現れたら必ず1になるという理解は、組み合わせ計算全般で役立つでしょう。特に、すべてを選ぶケースや何も選ばないケースでこの考え方が重要になります。
計算自体は非常にシンプルですが、0!の扱いと約分の理解が深まる良い例題といえるでしょう。
直感的な理解との整合性
公式による計算結果が、直感的な理解と一致することを確認しておきましょう。
| 視点 | 考え方 | 結果 |
|---|---|---|
| 直感的理解 | 8個全部を選ぶ方法は1つだけ | 1通り |
| 公式計算 | 8! / (8! × 0!) = 1 | 1通り |
| 補集合的理解 | 0個を残す方法は1つだけ | 1通り |
どの視点から考えても答えが1になることが分かります。数学の公式は直感と一致するように設計されているため、計算結果が直感と合っているかを確認する習慣をつけると良いでしょう。
もし計算結果が直感と大きく異なる場合は、計算ミスの可能性を疑うべきサインとなります。
組み合わせ計算の覚え方とコツ
続いては組み合わせ計算をマスターするためのコツを確認していきます。
特殊な組み合わせのパターン暗記
組み合わせには、覚えておくと便利な特殊なパターンがいくつか存在します。
– nC1 = n (1個選ぶ方法はn通り)
– nCn = 1 (全部選ぶ方法は1通り)
– nC(n-1) = n (n-1個選ぶ方法はn通り)
8C8はこの中のnCnのパターンに該当します。nがどんな値でも、nCnは必ず1になることを覚えておけば、瞬時に答えを導き出せるようになるでしょう。
特にnC0とnCnはどちらも答えが1になる点が興味深いですね。何も選ばない方法も、すべて選ぶ方法も、それぞれ1通りしかないという対称的な関係になっています。
0階乗の理解と重要性
0! = 1という定義は、組み合わせ計算において極めて重要な役割を果たします。
この定義がなければ、nC0やnCnといった特殊なケースで公式が使えなくなってしまうのです。0!を1と定めることで、すべての組み合わせが統一的な公式で計算できるようになります。
0!は約束事として1であると覚えてしまいましょう。「0から1まで掛け算する」という操作は存在しませんが、数学的な整合性のために1と定義されているのです。
| 階乗 | 値 | 計算式 |
|---|---|---|
| 0! | 1 | 定義により1 |
| 1! | 1 | 1 |
| 2! | 2 | 2×1 |
| 3! | 6 | 3×2×1 |
0!の理解は、組み合わせだけでなく、数列や微積分など様々な分野で必要になる基礎知識でしょう。
組み合わせと順列の違いの再確認
8C8と8P8の違いを理解することで、組み合わせの本質がより明確になります。
8P8 = 40320 (8個全部を並べる順列)
8C8は「8個すべてを選ぶ」という選択だけを考えるため1通りです。一方、8P8は「8個すべてを並べる順序」を考えるため、8! = 40320通りもの方法が存在します。
選ぶだけなのか、並べる順序まで考えるのかという違いが、この圧倒的な差を生み出すのです。組み合わせ(C)は順序を無視し、順列(P)は順序を重視するという基本原則を理解しておきましょう。
問題文に「選ぶ」とあれば組み合わせ、「並べる」「配置する」とあれば順列を使います。8C8のように全部を扱う場合でも、この区別は非常に重要になるでしょう。
8C8に関連する応用と考え方
続いては8C8を題材にした応用的な考え方を確認していきます。
確率問題での8C8の登場
8C8は確率計算の場面で重要な役割を果たすことがあります。
例えば、8個のボールがあり、そこから8個すべてを取り出す確率を考える問題では、8C8が分子または分母に登場するでしょう。この場合、8C8 = 1という値を正確に理解していることが重要です。
= (当たり8個から8個選ぶ組み合わせ) / (全体8個から8個選ぶ組み合わせ)
= 8C8 / 8C8
= 1 / 1
= 1 (確率100%)
このように、すべてを選ぶ状況では確率が1(100%)になることが多いです。8C8の理解は、こうした必然的な結果を論理的に導く際に役立ちます。
nCnの一般的な性質
8C8で学んだ考え方は、あらゆるnCnに応用できます。
nがどんな数であっても、nCn = 1という関係は常に成り立つのです。これは組み合わせの持つ普遍的な性質といえるでしょう。
| 組み合わせ | 意味 | 答え |
|---|---|---|
| 5C5 | 5個から5個すべて選ぶ | 1 |
| 10C10 | 10個から10個すべて選ぶ | 1 |
| 100C100 | 100個から100個すべて選ぶ | 1 |
| 1000C1000 | 1000個から1000個すべて選ぶ | 1 |
nがどれだけ大きくなっても、すべてを選ぶ方法は1通りしかないという本質は変わりません。この理解は、複雑な組み合わせ計算を簡略化する際に威力を発揮するでしょう。
二項定理との関連
8C8は二項定理においても重要な位置を占めています。
二項定理では、(a+b)のn乗を展開する際に組み合わせの係数が登場します。(a+b)^8を展開した式の最後の項には、8C8が係数として現れるのです。
二項定理の例(a+b)^8 = 8C0×a^8 + 8C1×a^7×b + … + 8C8×b^8
最後の項: 8C8×b^8 = 1×b^8 = b^8
8C8 = 1であることにより、最後の項は単にb^8となります。この性質は、二項展開の最初と最後の項の係数が常に1になる理由を説明しています。
nC0 = 1とnCn = 1という対称的な関係が、二項展開の美しい対称性を生み出しているのです。組み合わせの理解は、代数学の様々な分野につながっていくでしょう。
まとめ
8C8の計算方法と答えについて詳しく解説してきました。
8C8の答えは1であり、これは8個のものから8個すべてを選ぶ組み合わせの総数を表します。公式nCr = n! / (r! × (n-r)!)を使って計算すると、8! / (8! × 0!)となり、0! = 1を用いることで最終的に1という答えが導き出されるのです。
特に重要なポイントは、nCnという形の組み合わせは常に1になるという普遍的な性質でしょう。すべてを選ぶという行為には選択の余地がないため、どのような場合でも1通りしか存在しないのです。
また、0! = 1という定義の重要性も理解できました。この定義により、特殊なケースでも組み合わせの公式が統一的に機能するようになっています。
組み合わせの計算は、確率や場合の数、さらには二項定理など様々な数学的場面で活用される基礎的なスキルです。8C8のようなシンプルなケースを通じて本質を理解することで、より複雑な問題にも自信を持って取り組めるようになるでしょう。
この記事で紹介した考え方やコツを実践することで、組み合わせ計算の理解を深め、数学の実力向上につなげていきましょう。