数学の組み合わせ計算で登場する「8C6」という記号。一見すると複雑に見えますが、実は基本的なルールを理解すれば誰でも簡単に計算できるのです。
組み合わせの計算は、確率や場合の数を求める際に必須のスキルとなります。特に8C6のような具体的な数値を扱う問題は、高校数学の定期テストや大学入試でも頻出のテーマでしょう。
この記事では、8C6の計算方法から答えまでを丁寧に解説していきます。さらに、計算のコツや覚え方、そして「8C6と8C2が同じ値になる」という興味深い性質についても詳しく説明しますね。
組み合わせの計算が苦手な方でも、この記事を読めば8C6をスムーズに計算できるようになるはずです。それでは早速、8C6の基本的な意味と答えから確認していきましょう。
8C6の答えは28!組み合わせの基本原理を理解しよう
それではまず、8C6の計算結果とその基本的な意味について解説していきます。
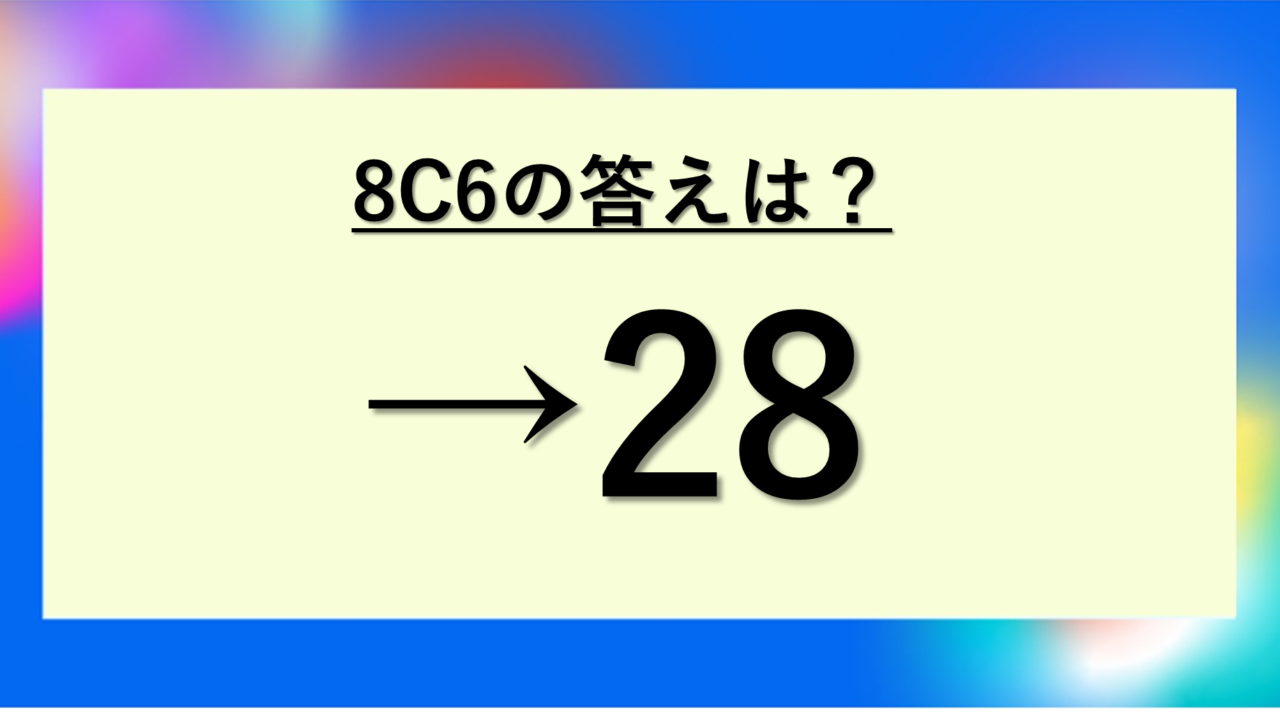
8C6の答えとその数学的な意味
この答えは、8個のものから6個を選ぶ組み合わせの総数を表しています。後ほど詳しい計算方法を解説しますが、まずはこの答えをしっかり覚えておきましょう。
組み合わせの問題では、選ぶ順番を考慮しないことがポイントになります。つまり、8個の中からどの6個を選ぶかだけが重要で、選んだ順序は関係ありません。
組み合わせ記号「nCr」の意味
8C6という記号は、「8個の中から6個を選ぶ組み合わせの数」を表す数学的な表記法です。
一般的にはnCrという形で表され、nは全体の個数、rは選ぶ個数を意味します。「C」は英語の「Combination(組み合わせ)」の頭文字から来ているのです。
読み方としては「8シー6」または「8コンビネーション6」と呼ばれます。数学の授業では前者の読み方が一般的でしょう。
8C6が表す具体的な状況
8C6は日常生活でも様々な場面で活用できる考え方です。
例えば、8人のグループから6人の委員を選ぶ場合の選び方の総数が8C6となります。また、8種類のトッピングから6種類を選んでピザを注文する際の組み合わせ数も同じく8C6で計算可能です。
このように、「いくつかの選択肢から特定の数を選ぶ」という状況で組み合わせの考え方が役立ちます。順番を気にせず、ただ「選ばれたかどうか」だけが重要な場面で使われるのが組み合わせの特徴ですね。
8C6の計算方法と求め方
続いては8C6の具体的な計算方法を確認していきます。
組み合わせの公式を使った計算
組み合わせの計算には、次の基本公式を使用します。
8C6 = 8! / (6! × 2!)
ここで「!」は階乗を表す記号です。階乗とは、その数から1まで順に掛け算していく計算方法を意味します。
例えば8! = 8×7×6×5×4×3×2×1となります。ただし、実際の計算ではすべての階乗を展開する必要はありません。効率的な計算方法を次に紹介しましょう。
実際の計算プロセス
8C6を効率的に計算する手順を見ていきます。
= (8×7×6!) / (6! × 2×1)
= (8×7) / (2×1)
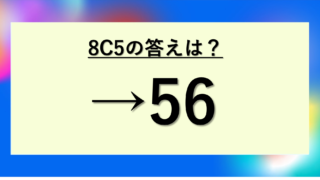
= 56 / 2
= 28
この計算では、分子と分母に共通する6!を約分しています。このテクニックにより、大きな数の階乗を計算せずに済むのがポイントです。
分母の2!は2×1=2となり、分子は8×7=56となります。最後に56÷2を計算して答えの28が導き出されますね。
計算ミスを防ぐチェックポイント
組み合わせの計算で間違いやすいポイントを確認しておきましょう。
| チェック項目 | 正しい方法 | 間違いやすい点 |
|---|---|---|
| 分母の計算 | r! × (n-r)!の両方を計算 | r!だけ計算して(n-r)!を忘れる |
| 約分のタイミング | 展開前に共通部分を約分 | すべて展開してから約分 |
| 階乗の計算 | 必要な部分だけ展開 | 全部を計算して数が大きくなる |
特に、分母にはr!と(n-r)!の両方が必要という点を忘れないようにしましょう。この部分を見落とすと、全く違う答えになってしまいます。
8C6と8C2が同じ値になる理由
続いては8C6と8C2の関係性について確認していきます。
補集合の関係による対称性
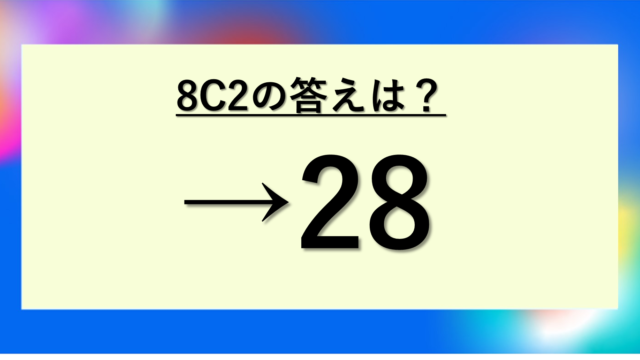
実は、8C6と8C2はどちらも答えが28で完全に一致します。これは偶然ではなく、組み合わせの重要な性質なのです。
nCr = nC(n-r)8C6 = 8C(8-6) = 8C2 = 28
この性質は「8個から6個を選ぶ」ことと「8個から2個を選ばない(残す)」ことが実質的に同じ意味を持つことから生まれます。
6個を選ぶということは、裏を返せば2個を選ばないということ。この発想の転換により、計算が簡単になる場合もあるのです。
実際の計算で確認
8C2を実際に計算して、本当に28になるか確認してみましょう。
= (8×7×6!) / (2×1×6!)
= (8×7) / 2
= 56 / 2
= 28
8C6の計算と途中式がほぼ同じになることに気づくでしょう。分子が8×7で、分母が2×1という点は完全に一致しています。
この性質を活用すれば、選ぶ数が多い場合は選ばない数で計算することで、より簡単に答えを導き出せますね。例えば10C9よりも10C1で計算した方が圧倒的に楽になります。
この性質を使った計算の工夫
組み合わせの対称性を理解すると、計算戦略を柔軟に選べるようになります。
一般的なルールとして、rとn-rのうち小さい方の数で計算すると効率的です。8C6の場合、6よりも2の方が小さいため、8C2として計算した方が楽になります。
| 組み合わせ | 変換後 | 計算の簡単さ |
|---|---|---|
| 10C8 | 10C2 | 8!より2!の方が簡単 |
| 7C5 | 7C2 | 5!より2!の方が簡単 |
| 12C10 | 12C2 | 10!より2!の方が簡単 |
この工夫を使えば、テストや入試での計算時間を大幅に短縮できるでしょう。
組み合わせ計算の覚え方とコツ
続いては組み合わせ計算をマスターするためのコツを確認していきます。
公式の覚え方と理解のポイント
組み合わせの公式を単に暗記するのではなく、意味を理解して覚えることが重要です。
nCr = n! / (r! × (n-r)!) という公式は、次のように考えると理解しやすくなります。まず、n個を1列に並べる方法がn!通りあります。しかし組み合わせでは順序を考えないため、選んだr個の並び替え(r!通り)と残りのn-r個の並び替え((n-r)!通り)で割る必要があるのです。
この理屈を理解すれば、公式を忘れても自分で導き出せるようになるでしょう。
計算スピードを上げる練習方法
組み合わせの計算を素早く正確に行うには、いくつかのパターンを覚えておくと便利です。
– nC1 = n (n個から1個選ぶ方法はn通り)
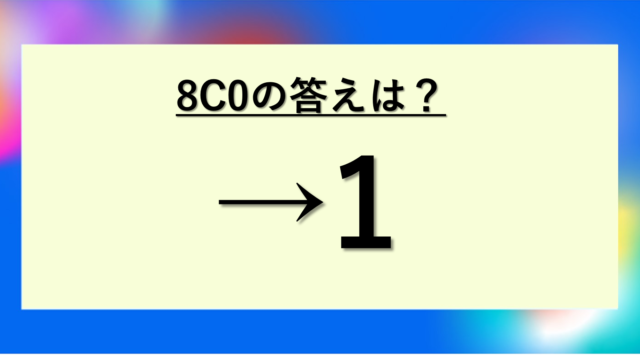
– nC0 = 1 (何も選ばない方法は1通り)
– nCn = 1 (全部選ぶ方法は1通り)
– nC2 = n(n-1)/2 (2個選ぶ公式)
特にnC2の形は頻出するため、n(n-1)/2という公式を覚えておくと計算が速くなります。8C2なら即座に8×7÷2=28と計算できますね。
また、約分できる部分を先に見つける習慣をつけると、計算ミスも減少します。展開してから約分するのではなく、展開前に約分可能な階乗を見つけましょう。
順列(P)との違いと使い分け
組み合わせ(C)と混同しやすいのが順列(P)です。この2つの違いをしっかり理解することが重要になります。
| 項目 | 組み合わせ(C) | 順列(P) |
|---|---|---|
| 順序 | 考慮しない | 考慮する |
| 8個から3個選ぶ | 8C3 = 56通り | 8P3 = 336通り |
| 具体例 | 委員3人を選ぶ | 会長・副会長・書記を選ぶ |
| 公式 | n!/(r!(n-r)!) | n!/(n-r)! |
問題文に「選ぶ」「取り出す」とあれば組み合わせ、「並べる」「順番に」とあれば順列を使うのが基本です。役職がある場合は順列、ない場合は組み合わせと覚えると分かりやすいでしょう。
8P6とすると20160通りになり、8C6の28通りとは大きく異なります。この違いを理解することで、問題の本質を見抜けるようになりますね。
まとめ
8C6の計算方法と答えについて詳しく解説してきました。
8C6の答えは28であり、これは8個のものから6個を選ぶ組み合わせの総数を表します。計算には公式nCr = n! / (r! × (n-r)!)を使用し、効率的に約分することで素早く答えを導き出せるのです。
特に重要なポイントは、8C6と8C2が同じ値になるという対称性でしょう。この性質を理解すれば、選ぶ数が多い場合でも簡単に計算できるようになります。
組み合わせの計算は、確率や場合の数を求める際の基礎となる重要なスキルです。公式の意味を理解し、約分のタイミングや対称性の活用といったテクニックを身につければ、より複雑な問題にも対応できるようになるでしょう。
この記事で紹介した計算方法やコツを実践することで、8C6のような組み合わせ計算をスムーズにこなせるはずです。数学の問題に自信を持って取り組んでいきましょう。