6C6の計算方法や答えは(数学の確率・場合の数・組み合わせ)? 求め方や覚え方のコツも!【なぜ】

数学の組み合わせの計算で「6C6」という表記を見たとき、どう考えればよいのか迷ったことはありませんか。6個のものから6個すべてを選ぶという状況は、一見すると不思議に感じるかもしれませんね。

実は、6C6は組み合わせの中でも特別な意味を持つ計算なんです。確率や場合の数の問題では、このような「全部を選ぶ」組み合わせが重要な役割を果たすことがあります。

この記事では、6C6の計算方法や答えについて、初心者の方にも分かりやすく丁寧に解説していきます。単なる計算手順だけでなく、なぜその答えになるのか、どう覚えればよいのか、さらにはnCnという一般的な形の組み合わせの性質についても詳しく紹介しますね。

6個から6個を選ぶというのは、言い換えれば「全部を選ぶ」ことと同じです。この状況では選び方は1通りしかないという直感的な理解が、数学的な計算とどうつながるのかを見ていきましょう。

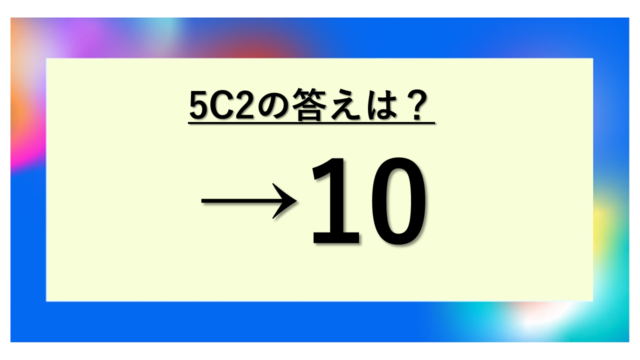
6C6の計算結果は1（なぜこの答えになるのか）

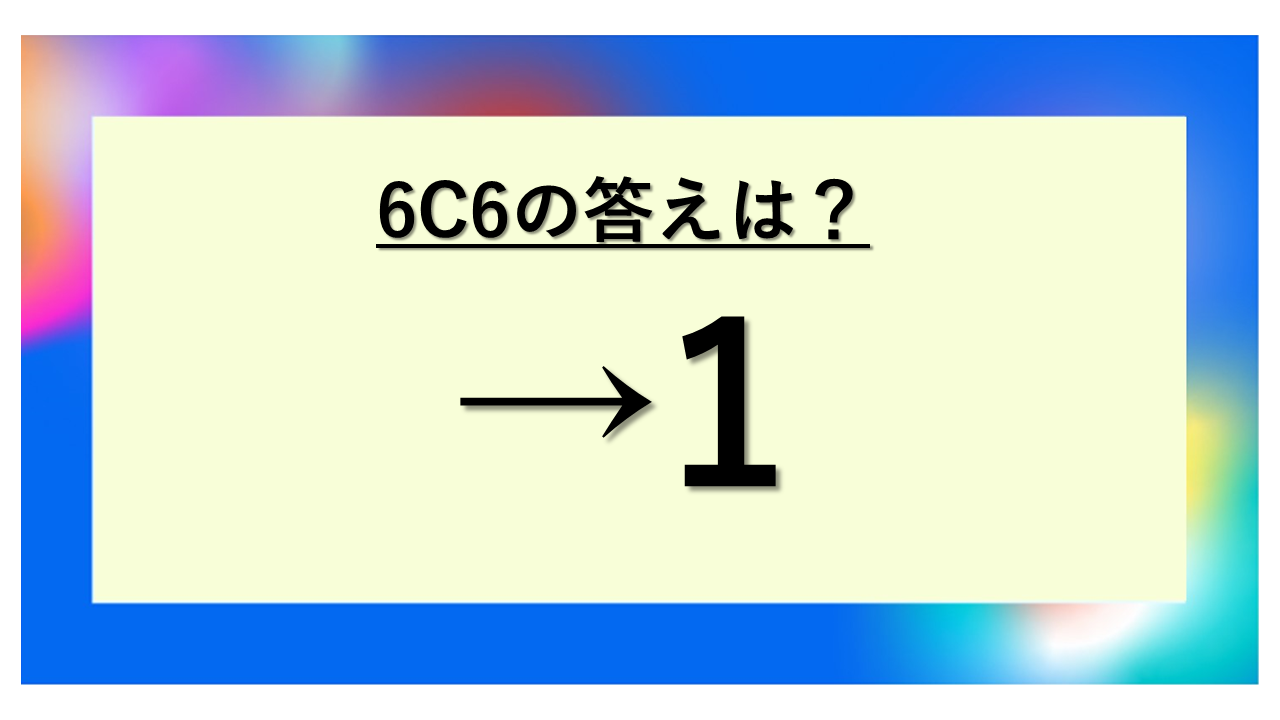
それではまず、6C6の計算結果と、その答えがなぜ1になるのかについて解説していきます。

6C6の答えは1になる理由

6C6の計算結果は1です。この数字は、6個のものから6個すべてを選ぶ組み合わせの総数を表しています。

なぜ1という答えになるのでしょうか。直感的に考えてみましょう。6個のものから6個すべてを選ぶということは、「全部を選ぶ」という意味です。

例えば、A、B、C、D、E、Fという6つの要素があるとき、6個すべてを選ぶ方法は何通りあるでしょうか。

組み合わせでは順序を考慮しないため、全部を選ぶ方法はただ1通りしか存在しないんです。ABCDEFを選ぶのと、FEDCBAを選ぶのは同じ選び方として扱われますからね。

これは日常的な感覚とも一致するでしょう。例えば「6人のクラス全員を遠足に連れて行く方法は何通りか」と聞かれたら、当然1通りですよね。全員を連れて行くという選択肢は1つしかないわけです。

nCnが常に1になる数学的理由

6C6=1という結果は、より一般的なnCn=1という法則の具体例です。この性質について、数学的な観点から見ていきましょう。

組み合わせの公式を使って計算してみます。

階乗の定義において、0!=1という特別な約束があります。これは一見不思議に思えるかもしれませんが、組み合わせの計算が矛盾なく成り立つために必要な定義なんです。

6C6を実際に計算してみましょう。

分子と分母が同じ値になるため、約分すると1になりますね。この計算からも、nCnは必ず1になることが分かるでしょう。

対称性から見る6C6と6C0の関係

組み合わせには対称性という重要な性質があります。この性質を使うと、6C6について別の視点から理解できるんです。

対称性の法則nCr=nC(n-r)を6C6に適用してみましょう。

「全部を選ぶことと何も選ばないことが同じ数」というのは不思議に感じるかもしれません。しかし、どちらも選択肢が1つしかないという点で共通しているんですね。

組み合わせ	意味	答え	理由
6C0	何も選ばない	1	方法は1通りだけ
6C6	全部選ぶ	1	方法は1通りだけ
nC0	何も選ばない	1	一般的に常に1
nCn	全部選ぶ	1	一般的に常に1

この対称性の理解は、組み合わせの本質を深く理解することにつながるでしょう。両端の極端なケース(何も選ばない、全部選ぶ)が同じ値を取るというのは、数学の美しさを感じさせますね。

6C6の計算方法と求め方の手順（公式の使い方）

続いては、6C6の具体的な計算方法と求め方の手順を確認していきます。

組み合わせの基本公式と6C6への適用

6C6を計算するには、組み合わせの公式を正しく理解することが大切です。一般的に、n個からr個を選ぶ組み合わせは「nCr」と表記され、次の公式で計算できますよ。

ここで重要なのが、0!の値です。階乗の定義において、0!=1と定められています。これは約束事として覚えておく必要があるでしょう。

なぜ0!=1と定義されているのでしょうか。これは、組み合わせや順列の公式が整合性を持って機能するために必要な定義なんです。もし0!=0や他の値だったら、nCnの計算が正しく行えなくなってしまいますからね。

実際に6C6を計算してみましょう。

このように、分子と分母が同じ値になるため、答えは必ず1になるんですね。

最も簡単な理解方法（直感的アプローチ）

6C6を計算する最も簡単な方法は、公式に頼らず直感的に考えることです。数式を見る前に、状況の意味を理解しましょう。

具体的な状況で考えてみます。

この直感的理解があれば、nCnという形を見た瞬間に答えは1だと分かるようになります。計算する必要すらないわけですね。

特に試験などでは、時間が限られています。6C6のような特殊なケースを見たら、すぐに「これは全部選ぶケースだから答えは1」と判断できることが重要でしょう。

暗記すべき特殊なケースをまとめておきます。

形	意味	答え	覚え方
nC0	何も選ばない	1	選択肢は1つだけ
nC1	1個だけ選ぶ	n	n通りの選び方
nC(n-1)	1個だけ残す	n	nC1と同じ
nCn	全部選ぶ	1	選択肢は1つだけ

これらの特殊なケースを覚えておけば、計算時間を大幅に短縮できますよ。

階乗を使った詳しい計算過程

数学的な理解を深めるために、階乗を使った詳しい計算過程も確認しておきましょう。

まず、階乗の定義を復習します。

0!だけは計算ではなく定義によって1と決められています。これは組み合わせや順列の公式が美しく統一されるために必要な約束事なんですね。

6C6の計算を段階的に進めてみましょう。

この計算過程で重要なのは、分子と分母の6!が約分されるという点です。実際には720という大きな数を計算する必要はなく、6!÷6!=1と直接分かるんですね。

電卓や計算ツールを使う場合でも、手順は同じです。関数電卓なら「6」→「nCr」→「6」→「=」と押せば1と表示されます。Excelなら「=COMBIN(6,6)」と入力すれば計算できるでしょう。

ただし、試験ではnCn=1という性質を理解していることが評価されることも多いです。単に計算できるだけでなく、なぜその答えになるのかを説明できることが大切ですよ。

6C6の覚え方のコツと組み合わせの重要な性質

続いては、6C6の覚え方のコツと、組み合わせの重要な性質について確認していきます。

特殊な組み合わせの覚え方

6C6のような特殊な組み合わせを効率的に覚えるコツは、意味と結びつけて理解することです。単に「nCnは1」と暗記するのではなく、なぜそうなるのかを理解しましょう。

まず、組み合わせの両端のケースを整理します。

この「選択の余地がない」という視点が重要です。何も選ばない場合も、全部選ぶ場合も、実質的に選択肢は1つしかないわけですね。

パスカルの三角形で視覚的に理解することもできます。

最下段を見てください。両端が1になっていますね。これが6C0=1と6C6=1を表しています。パスカルの三角形の両端は常に1という性質があるんです。

このパターンを覚えておけば、どんな数のnCnでも瞬時に答えは1だと分かるでしょう。

組み合わせの恒等式と性質

組み合わせには、様々な恒等式や性質があります。これらを知っておくと、計算を楽にしたり、問題を解く際のヒントになったりしますよ。

重要な性質をまとめてみましょう。

特に性質4は、パスカルの三角形を作る際の規則です。例えば6C6 + 7C0 = 7C1という関係があります。実際に計算してみると、1 + 1 ≠ 7となり、あれ?と思うかもしれません。

実は正しくは、5C5 + 5C6 = 6C6です。ただし5C6は定義されないので0とみなすと、1 + 0 = 1となって成り立ちますね。

また、組み合わせの総和にも面白い性質があります。

この性質は、各要素を「選ぶ」か「選ばない」かの2通りの選択が6個あるため、全体で2^6通りになるという考え方から導かれます。6C6はその中の1パターンというわけですね。

nCnが現れる実際の場面

nCn=1という性質は、実際の問題でどのように使われるのでしょうか。具体的な場面を見てみましょう。

確率の問題では、分母にnCnが現れることがあります。

また、場合の数を数える際に、「全体からある条件を満たす場合を引く」という余事象の考え方で、「全体」を表す数としてnCnが登場することがあります。

場面	使い方	具体例
全選択	全部選ぶ場合の数	6C6 = 1
確率の分母	全体の場合の数	n個から全部選ぶ
恒等式の検証	境界条件として	nCn = 1を確認
組み合わせの和	終点として	Σの最後の項

実務的には、nCnが直接登場する場面は多くないかもしれません。しかし、組み合わせの理論を理解する上で重要な概念であることは間違いないでしょう。

6C6が登場する確率・場合の数の問題例

続いては、6C6が実際にどのような場面で使われるのか、具体的な問題例を通して確認していきます。

代表的な6C6の応用問題と解法

6C6が登場する問題は、主に「全部を選ぶ」場合や確率の計算で現れます。実際の問題を見てみましょう。

この問題は非常にシンプルですね。全員を選ぶという選択肢は1つしかないため、答えは1通りです。

もう少し実践的な問題も見てみましょう。

この問題では、分母と分子が両方とも6C6になっています。赤玉しか入っていないため、どう選んでも必ず赤玉になり、確率は100%になるわけですね。

実際の試験では、もう少し複雑な形で6C6が登場することが多いでしょう。

組み合わせの総和を使った問題

6C6は、組み合わせの総和を計算する際の最後の項として登場することがあります。

この問題では、6C6が「全部ONにする」場合を表しています。組み合わせの総和の公式を使えば、すぐに2^6=64と計算できますが、6C6を含めた全ての項を足しても同じ答えになるんですね。

別の視点からの問題も見てみましょう。

ここでも6C6は「全部買う」という選択肢を表していますね。

確率計算での6C6の役割

確率の問題では、6C6が分母や分子に現れることがあります。特に「全体の場合の数」として使われることが多いでしょう。

この問題は少しトリッキーですね。全部選べば必ず6が含まれるため、確率は100%になります。

もう少し複雑な例も見てみましょう。

問題タイプ	6C6の役割	ポイント
全選択	選ぶ方法の数	答えは常に1
確率の分母	全体の場合の数	全部選ぶケース
組み合わせの和	最後の項	総和=2^n
恒等式の検証	境界条件	公式の確認

6C6自体は単純な計算ですが、問題の文脈の中でどう使われるかを理解することが重要でしょう。特に確率の問題では、分母と分子にそれぞれ組み合わせが現れることが多いため、どの部分が6C6に対応するのかを正確に把握する必要がありますよ。

まとめ

6C6の計算方法と答え、そしてその意味について詳しく解説してきました。重要なポイントをまとめておきましょう。

6C6の答えは1であり、これは6個のものから6個すべてを選ぶ組み合わせの総数を表しています。全部を選ぶ方法は1通りしかないという直感的な理解が、数学的な計算結果と一致しているんですね。

一般的に、nCnは常に1になります。これは組み合わせの公式nCn=n!÷(n!×0!)において、0!=1という定義により、分子と分母が約分されて1になるためです。また、対称性の法則からnCn=nC0=1という関係も理解できるでしょう。

計算方法としては、公式を使って計算することもできますが、最も効率的なのは「全部選ぶ方法は1通り」と直感的に理解することです。nCnという形を見た瞬間に答えは1だと判断できるようになれば、試験時間の大幅な短縮につながります。

6C6のような特殊なケース(nC0、nC1、nCn)を覚えておくことは、組み合わせの計算を効率化するだけでなく、組み合わせの本質的な理解を深めることにもつながるでしょう。これらの基本をしっかり押さえて、確率や場合の数の様々な問題に対応できる力を身につけていってください。