5C5の計算方法や答えは(数学の確率・場合の数・組み合わせ)? 求め方や覚え方のコツも!【なぜ】

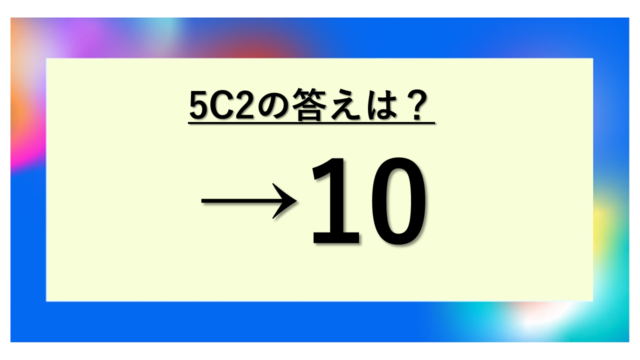
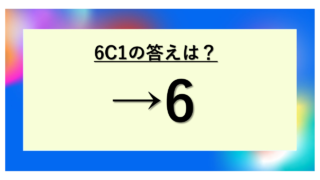
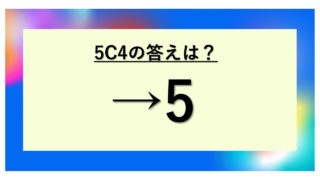
数学の組み合わせの問題では、「5C5」という表記を見かけることがあるでしょう。一見すると複雑に見えるかもしれませんが、実はこの計算には明確なルールがあり、理解すれば簡単に答えを導き出せます。

特に確率や場合の数を扱う問題では、組み合わせの計算が頻繁に登場するため、しっかりとした理解が求められるでしょう。5C5のような特殊なケースは、一般的な組み合わせの計算とは少し異なる特徴を持っています。

本記事では、5C5の計算方法や答え、さらには求め方のコツや覚え方まで、数学が苦手な方にもわかりやすく解説していきます。なぜその答えになるのかという理由も含めて、丁寧に説明していきますので、ぜひ最後までご覧ください。

5C5の答えは1！その理由と計算の基本

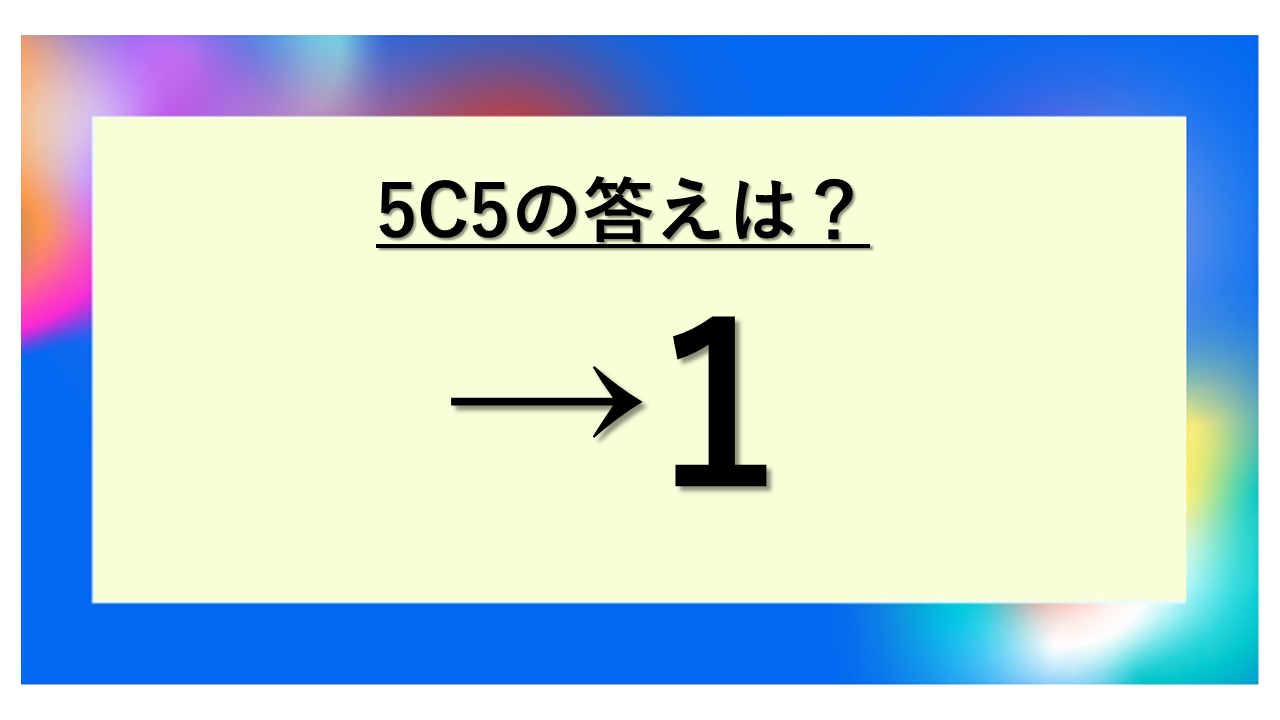
それではまず、5C5の答えと、なぜそうなるのかについて解説していきます。

5C5の計算結果とその意味

組み合わせ（Combination）は、異なるn個のものからr個を選ぶ場合の数を表す概念でしょう。5C5の場合、5個すべてを選ぶわけですから、選び方は「全部選ぶ」という1通りしかありません。

例えば、りんご、みかん、バナナ、ぶどう、いちごという5種類の果物があったとき、この5種類すべてを選ぶ方法は1つだけ。どの順番で選んでも、最終的に手元にあるのは同じ5種類の果物になるのです。

これは直感的にも理解しやすい結果ではないでしょうか。全部を選ぶのですから、選択の余地がないということですね。

組み合わせnCrの基本公式

組み合わせの計算には、基本となる公式があります。

この公式を5C5に当てはめてみましょう。n=5、r=5なので、次のようになります。

ここで重要なポイントは、0!（0の階乗）は1と定義されているということ。これは数学的な約束事であり、この定義があるからこそ組み合わせの公式が成り立つのです。

なぜ5C5が1になるのか？直感的な理解

計算式だけでなく、直感的にも5C5=1を理解しておくことが大切でしょう。

5個のものから5個を選ぶということは、「全部選ぶ」か「全部選ばない」かの2択ではなく、「全部選ぶ」という選択肢しかない状況です。何も残さずすべてを取るわけですから、選び方のバリエーションは存在しません。

これを日常生活に例えると、5人家族全員で旅行に行く方法を考えるようなもの。全員で行くという選択肢は1つだけであり、誰を連れて行くか選ぶ余地はないのです。

このように、nCn（n個からn個を選ぶ組み合わせ）は常に1になるという法則が成り立ちます。3C3も、10C10も、100C100も、すべて答えは1になるでしょう。

5C5の計算方法を段階的に解説

続いては、5C5を実際に計算する方法を段階的に確認していきます。

階乗の計算を理解する

組み合わせの計算では、階乗（factorial）の理解が欠かせません。

階乗は「!」という記号で表され、その数以下のすべての正の整数を掛け合わせたものです。

特に重要なのは、0! = 1と定義されていること。これは一見不思議に思えるかもしれませんが、組み合わせや順列の公式を矛盾なく成り立たせるための数学的な約束事なのです。

5C5の計算では5!が登場しますので、120という数値をしっかり覚えておくとよいでしょう。

公式に当てはめて計算する手順

実際に公式を使って5C5を計算してみましょう。

ステップ	計算内容	結果
1. 公式の確認	5C5 = 5! / (5! × 0!)	–
2. 階乗の計算	5! = 120、0! = 1	120、1
3. 分子の計算	5! = 120	120
4. 分母の計算	5! × 0! = 120 × 1	120
5. 最終計算	120 / 120	1

この手順を踏めば、確実に正しい答えにたどり着けます。重要なのは、各ステップを丁寧に計算していくことでしょう。

特に分母の計算で0!が登場することに注意が必要です。0!を0と間違えてしまうと、計算が成り立たなくなってしまいます。

簡単な覚え方とショートカット

毎回公式通りに計算するのは時間がかかるため、いくつかの覚え方やショートカットを知っておくと便利です。

これらのパターンを覚えておけば、わざわざ計算しなくても瞬時に答えが分かるでしょう。特にnCnは頻出パターンなので、「全部選ぶなら1通り」と覚えておくことをおすすめします。

また、対称性の法則としてnCr = nC(n-r)という関係も成り立ちます。例えば5C2 = 5C3という具合ですね。これは「5個から2個選ぶ」ことと「5個から3個選んで残す（＝2個選ばない）」ことが同じだからです。

組み合わせと順列の違いと使い分け

続いては、組み合わせと似た概念である順列との違いを確認していきます。

組み合わせ（Combination）の特徴

組み合わせは、選ぶ順序を考慮しない場合の数を求める方法です。

例えば、A、B、Cという3人から2人を選ぶ組み合わせを考えてみましょう。

この場合、「AとBを選ぶ」ことと「BとAを選ぶ」ことは同じとみなされます。つまり、選ばれた結果だけが重要で、どの順番で選んだかは関係ないということですね。

チームを作る、委員を選ぶ、トッピングを選ぶといった場面では、この組み合わせの考え方が使われるでしょう。

順列（Permutation）の特徴

一方、順列は選ぶ順序も考慮する場合の数を求める方法です。

同じくA、B、Cという3人から2人を選ぶ順列を考えてみます。

順列では「AとB」と「BとA」は別のものとして数えられます。1位と2位を決める、席順を決める、並び順を決めるといった場面では、この順列の考え方が必要になるでしょう。

順列の公式はnPr = n! / (n-r)!で表されます。組み合わせの公式と似ていますが、分母にr!がない点が異なるのです。

5C5と5P5の違いを比較

5C5と5P5を比較すると、両者の違いがより明確になります。

項目	5C5（組み合わせ）	5P5（順列）
意味	5個から5個を選ぶ（順序無関係）	5個から5個を並べる（順序重要）
公式	5! / (5! × 0!)	5! / 0!
計算結果	1	120
具体例	5人全員をチームに選ぶ	5人を一列に並べる

5C5は「全員を選ぶ」だけなので1通りですが、5P5は「全員を並べる」ので120通りにもなるのです。この違いを理解することが、確率や場合の数の問題を解く上で非常に重要でしょう。

問題文に「選ぶ」とあれば組み合わせ、「並べる」「順位をつける」とあれば順列を使うと判断できます。

実際の問題での5C5の応用例

続いては、5C5が実際の問題でどのように使われるかを確認していきます。

確率の問題における5C5

確率の問題では、組み合わせの考え方が頻繁に登場します。

この問題では、5個の玉から5個を選ぶ方法が5C5=1通り、そしてその1通りがすべて赤玉という条件を満たしています。したがって、確率は1/1=1、つまり100%の確率ですべて赤玉ということになるでしょう。

もう少し複雑な例も見てみましょう。

この場合、5個すべてを取り出すわけですから、取り出し方は5C5=1通りのみ。つまり、どのように取り出しても「赤玉3個、白玉2個」という結果になるのです。

トーナメントや選択問題での活用

5C5は、実生活に近い場面でも活用されます。

例えば、5人の候補者全員を委員会メンバーに選ぶ場合を考えてみましょう。この選び方は5C5=1通りしかありません。つまり、全員を選ぶという決定には選択の余地がないということですね。

また、5つの議題すべてを議論する会議の進め方を考える際も、どの議題も漏らさず扱うという意味で5C5=1の概念が当てはまります。

逆に言えば、5つの選択肢から一部だけを選ぶ場合（例えば5C3など）には複数の選び方が存在するということ。この対比を理解することで、問題の構造をより深く把握できるでしょう。

nCnが1になる一般的なケース

5C5だけでなく、nCn全般について理解を深めておくことが重要です。

この法則の実用的な意味は、「すべてを選ぶ方法は1つしかない」という当たり前のことを数学的に表現しているということ。

例えば、クラス全員で遠足に行く、本棚の本をすべて読む、商品をすべて購入するといった状況では、必ずnCn=1の考え方が背景にあるのです。

逆に、nC0（何も選ばない）も1になるという対称性も興味深いでしょう。何も選ばない方法も実は1通りしかないという考え方ですね。

まとめ

5C5の計算方法と答えについて、詳しく解説してきました。

5C5の答えは1であり、これは5個のものから5個すべてを選ぶ方法が1通りしかないことを意味しています。計算式としては5! / (5! × 0!) = 120 / 120 = 1となり、0!=1という定義が重要な役割を果たしているのです。

組み合わせnCrの基本公式を理解し、階乗の計算方法を身につけることで、5C5だけでなく様々な組み合わせの問題に対応できるようになるでしょう。特にnCn=1という法則は、「全部選ぶなら1通り」と直感的に覚えておくことをおすすめします。

また、組み合わせと順列の違いを理解することも大切です。5C5は1通りですが、5P5は120通りになるという違いは、順序を考慮するかしないかによって生じるもの。問題文をよく読んで、どちらを使うべきか判断する力を養いましょう。

確率や場合の数の問題では、5C5のような特殊なケースが頻出します。公式を機械的に暗記するだけでなく、その意味を理解することで、応用力が身につき、数学がより楽しくなるはずです。