5C0の計算方法や答えは（数学の確率・場合の数・組み合わせ）？求め方や覚え方のコツも！【なぜ】

数学の確率や場合の数を学習していると、「5C0」という表記に出会うことがあるでしょう。この組み合わせの計算は、一見すると「5個から0個選ぶってどういうこと？」と疑問に思う方も多いのではないでしょうか。

実は5C0のような「0個選ぶ組み合わせ」には、数学的に重要な意味が隠されています。単なる計算問題としてではなく、その背景にある考え方を理解することで、組み合わせの本質が見えてくるはずです。

本記事では、5C0の計算方法や答え、そしてなぜその値になるのかについて、初心者の方にもわかりやすく解説していきます。計算の手順だけでなく、覚え方のコツや実際の応用例まで、丁寧に確認していきましょう。

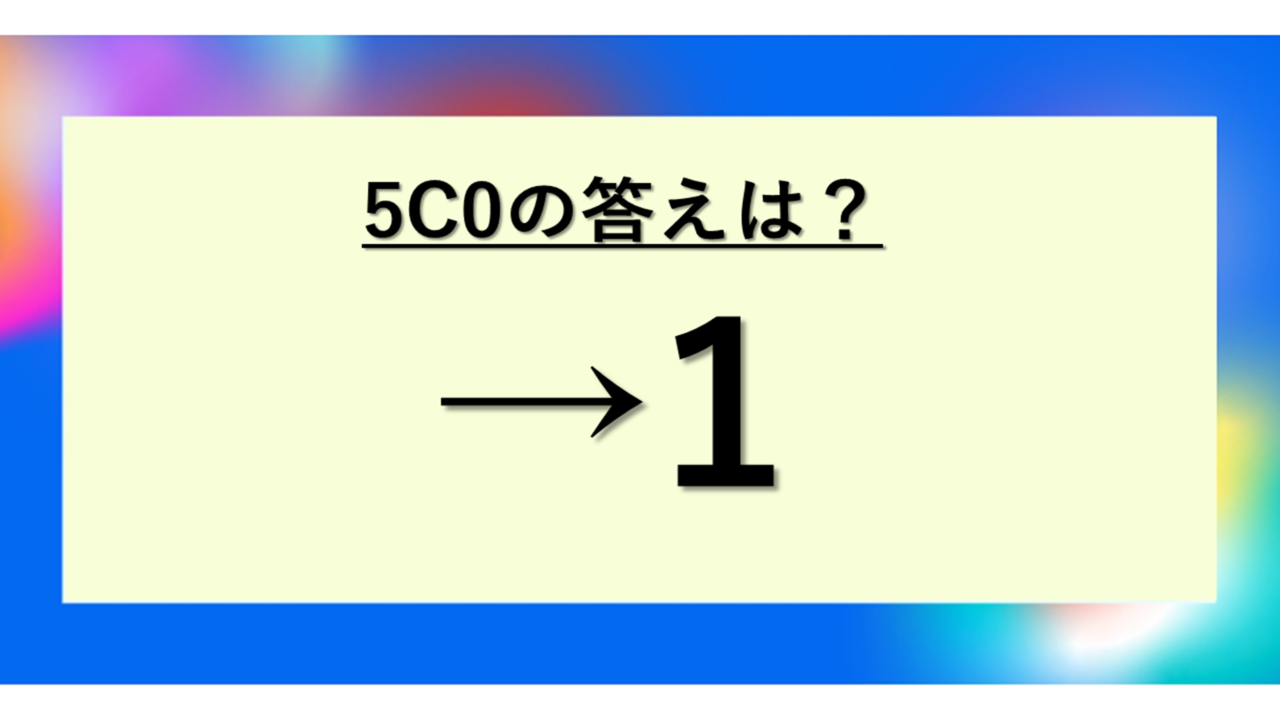
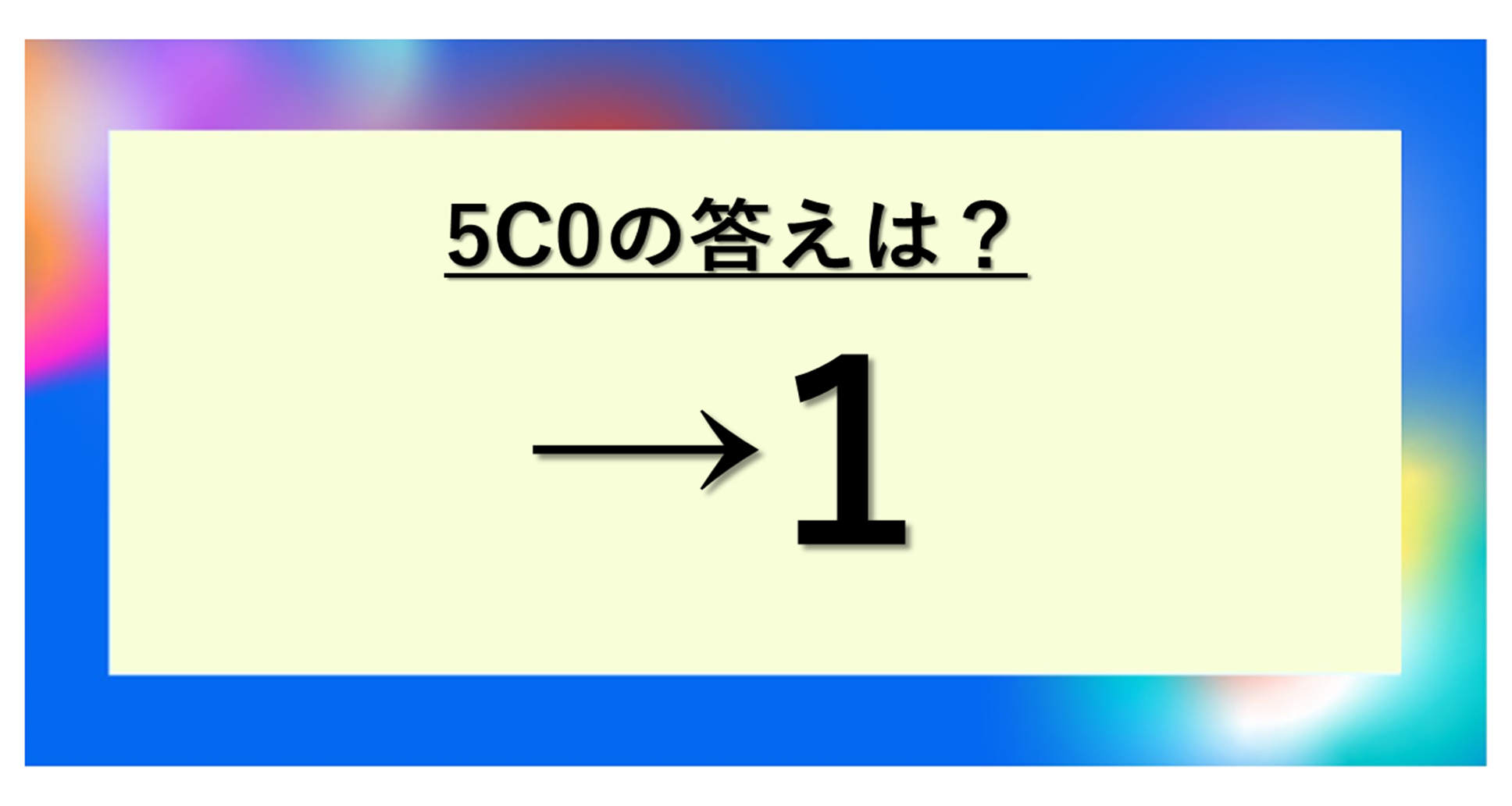
5C0の答えは1！その理由と数学的な意味

それではまず、5C0の答えとその理由について解説していきます。

5C0の計算結果とその値

結論から申し上げると、5C0の答えは1になります。これは「5個のものから0個を選ぶ組み合わせの数」を意味していますが、直感的には少し不思議に感じるかもしれません。

数学において、nC0（n個から0個選ぶ組み合わせ）は常に1となる重要な性質があります。これは5C0に限らず、10C0でも100C0でも同じです。

なぜ0個選ぶのに答えが1なのか

「何も選ばないのに1通りある」という考え方は、最初は理解しにくいかもしれません。しかし、これには明確な数学的理由があります。

「何も選ばない」という選択自体が1つの方法だからです。例えば、5つの果物があるとき、「1つも選ばない」という行為は、確かに1通りの方法として存在していますよね。

また、階乗を使った公式で計算すると、0!=1（0の階乗は1）という定義により、自然に答えが1になります。この定義は、組み合わせや順列の公式が美しく成り立つために必要不可欠なものなのです。

組み合わせにおける空集合の考え方

数学的には、5C0は「空集合」という概念と密接に関係しています。空集合とは、要素を1つも含まない集合のことです。

5個の要素から0個選ぶということは、空集合を作る方法が何通りあるかを問うているのと同じ意味になります。空集合は1つしか存在しないため、その作り方も1通りというわけです。

この考え方は、確率論や集合論において非常に重要な基礎となっています。一見すると抽象的に思えるかもしれませんが、組み合わせの理論全体を支える土台の一つなのです。

5C0の計算方法と公式の使い方

続いては、5C0を実際に計算する方法を確認していきます。

組み合わせの基本公式

組み合わせnCrを計算する基本公式は以下の通りです。

この公式に5C0を当てはめると、n=5、r=0となります。それでは実際に計算してみましょう。

階乗の定義を確認すると、5!=5×4×3×2×1=120、0!=1（定義により）となります。この0!=1という定義は、組み合わせの計算において極めて重要な役割を果たしているのです。

5C0の具体的な計算手順

公式に数値を代入して、丁寧に計算していきます。

このように、分子と分母に同じ5!が現れて約分されるため、結果は1になります。0!=1という定義があるからこそ、この計算が成り立つわけです。

計算の各ステップを見ると、非常にシンプルな構造になっていることがわかるでしょう。実は、どんな数nに対しても、nC0の計算は同じパターンで必ず1になるのです。

電卓や計算ツールでの確認方法

現代では、関数電卓やスマートフォンの計算アプリでも組み合わせを計算できます。多くの計算機では「nCr」や「C」というボタンがあり、これを使うことで簡単に答えを求められるでしょう。

操作方法は機種によって異なりますが、一般的には「5」→「nCr」→「0」→「=」の順に入力します。結果は当然1と表示されるはずです。

ただし、計算ツールに頼るだけでなく、なぜその答えになるのかを理解することが数学の学習では非常に大切になります。公式の意味を理解していれば、応用問題にも対応できるようになるでしょう。

組み合わせnC0が常に1になる理由と覚え方のコツ

続いては、nC0が常に1になる性質について、さらに深く確認していきます。

nC0=1が成り立つ数学的証明

nC0が常に1になることは、組み合わせの公式から厳密に証明できます。

この証明は、nがどんな自然数であっても成り立ちます。5だけでなく、10でも1000でも、同じ論理で答えは1になるのです。

また、別の角度から考えると、「選ばない」という行為は常に1通りしかないという直感的な理解とも一致しています。数学の美しさは、こうした厳密な計算と直感的な理解が一致する点にあるのではないでしょうか。

覚え方の実用的なコツとテクニック

nC0=1を覚えるコツはいくつかあります。最も簡単な方法は、「何も選ばない方法は1通り」と言葉で覚えることでしょう。

また、組み合わせの対称性nCr = nC(n-r)を利用する方法もあります。例えば、5C0 = 5C5 となりますが、5C5は「5個全部選ぶ」方法なので明らかに1通りです。この対称性を使えば、nC0が1であることが自然に理解できるはずです。

さらに、パスカルの三角形を思い浮かべる方法もあります。パスカルの三角形の両端は常に1ですが、これはnC0とnCnに対応しています。視覚的なイメージとして記憶しておくと、忘れにくくなるでしょう。

他のnCrとの関係性と比較

5C0を他の組み合わせと比較すると、理解がさらに深まります。

組み合わせ	計算式	答え	意味
5C0	5!/(0!×5!)	1	5個から0個選ぶ
5C1	5!/(1!×4!)	5	5個から1個選ぶ
5C2	5!/(2!×3!)	10	5個から2個選ぶ
5C3	5!/(3!×2!)	10	5個から3個選ぶ
5C4	5!/(4!×1!)	5	5個から4個選ぶ
5C5	5!/(5!×0!)	1	5個から5個選ぶ

この表を見ると、5C0と5C5が対称的に1になっていることがわかります。また、5C1と5C4、5C2と5C3も対称的に同じ値です。この対称性はnCr = nC(n-r)という重要な性質から来ています。

確率や場合の数における5C0の実践的な応用

続いては、5C0が実際にどのような場面で使われるのかを確認していきます。

確率計算での5C0の役割

確率の問題では、「少なくとも1つ」や「全部」といった条件が出てくることがよくあります。このとき、5C0が間接的に重要な役割を果たすのです。

例えば、「5回のコイン投げで、少なくとも1回は表が出る確率」を求める場合を考えてみましょう。この問題は、余事象（1回も表が出ない確率）を使って解くのが効率的です。

ここで「1回も表が出ない」というのは、ある意味で「表を0回選ぶ」ことに相当します。このような計算の背景には、nC0の考え方が潜んでいると言えるでしょう。

二項定理における5C0の位置づけ

二項定理は、(a+b)^nを展開するときに組み合わせの係数が現れる重要な定理です。

この展開式の最初の項で、係数として5C0=1が登場しています。二項定理は確率論や統計学の基礎となる重要な定理であり、組み合わせの計算が実際の数学でどれほど重要かを示す好例でしょう。

特に、二項分布や正規分布といった統計学の中心的な概念も、この二項定理と組み合わせの理論に基づいているのです。

場合の数の問題での具体例

実際の場合の数の問題で、5C0がどのように使われるかを見てみましょう。

「5種類の果物があるとき、少なくとも1種類は選ぶ方法は何通りあるか」という問題を考えます。全体の選び方から「0種類選ぶ」場合を引けば答えが出るでしょう。

このように、「少なくとも1つ」という条件を扱うときに、nC0が重要な役割を果たします。余事象の考え方と組み合わせることで、複雑な問題も簡潔に解けるようになるのです。

また、確率や統計の分野では、「事象が起こらない確率」を計算する際にも、0個選ぶという概念が頻繁に登場します。一見すると地味に見える5C0ですが、実は数学の様々な場面で活躍している重要な概念なのです。

まとめ

本記事では、5C0の計算方法や答え、そしてその数学的な意味について詳しく解説してきました。

組み合わせの公式nCr = n!/(r!×(n-r)!)に5C0を代入すると、0!=1という定義により、分子と分母が約分されて答えは1になります。この結果は、nがどんな自然数であっても成り立つ普遍的な性質です。

nC0が常に1になることを理解することは、組み合わせや確率の学習において非常に重要な基礎となります。二項定理や余事象を使った確率計算など、様々な応用場面で5C0の概念が活用されているのです。

覚え方のコツとしては、「何も選ばない方法は1通り」という言葉での理解、組み合わせの対称性nCr = nC(n-r)を利用した理解、そしてパスカルの三角形での視覚的なイメージなどが効果的でしょう。

数学は単なる計算だけでなく、その背後にある論理や概念を理解することで、より深く楽しく学ぶことができます。5C0という一見シンプルな計算にも、組み合わせ論の美しい構造が隠されているのです。