4C2の計算方法や答えは(数学の確率・場合の数・組み合わせ)? 求め方や覚え方のコツも!【なぜ】

数学の問題を解いていて、4C2という表記を見かけたことはありませんか。

組み合わせの計算は、確率や場合の数を求める際に欠かせない重要な概念です。特に高校数学では頻繁に登場するため、しっかりと理解しておく必要があるでしょう。

4C2は「4個のものから2個を選ぶ組み合わせの数」を表しており、日常生活でも実は多く使われています。例えば、4人のグループから2人の代表を選ぶ方法や、4種類のトッピングから2つを選ぶパターンなど、身近な場面で活用できる考え方なのです。

本記事では、4C2の計算方法を基礎から丁寧に解説していきます。公式の使い方はもちろん、なぜその公式が成り立つのかという理論的な背景、さらには覚え方のコツまで詳しくご紹介します。

数学が苦手な方でも理解できるよう、具体例を交えながら分かりやすく説明していきますので、ぜひ最後までお読みください。

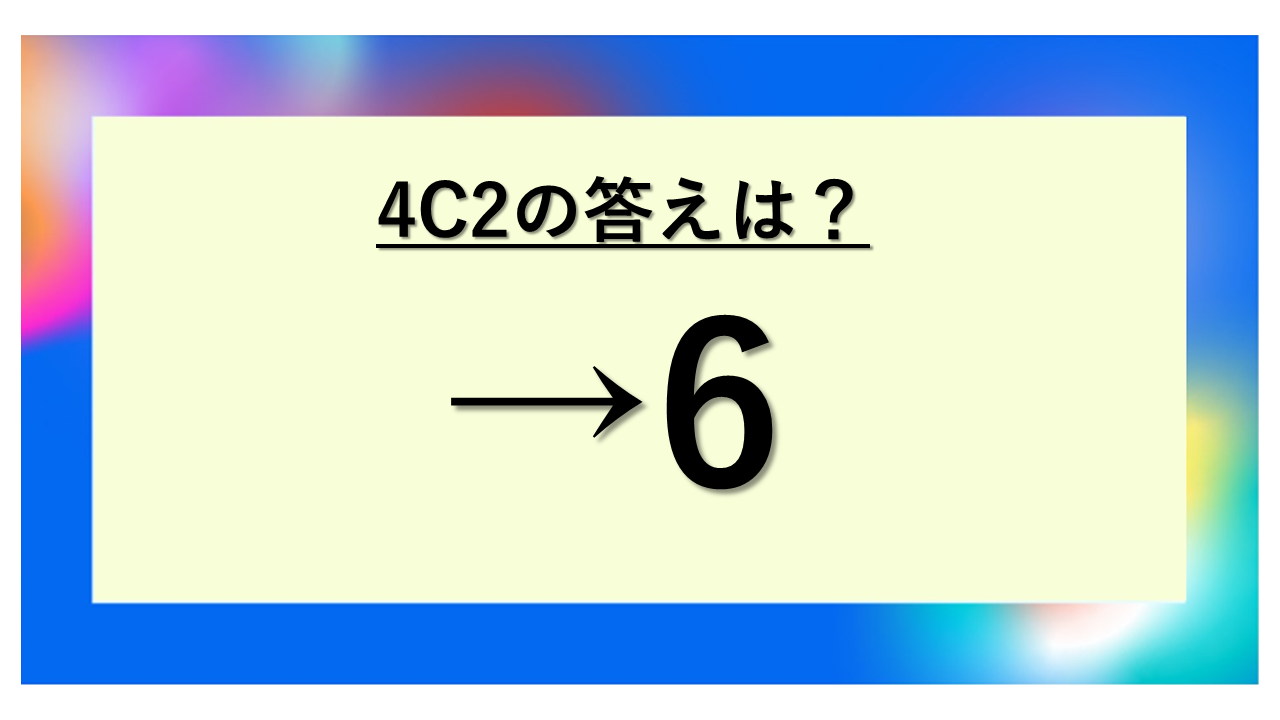
4C2の答えは6!計算結果と意味を理解しよう

それではまず、4C2の答えと基本的な意味について解説していきます。

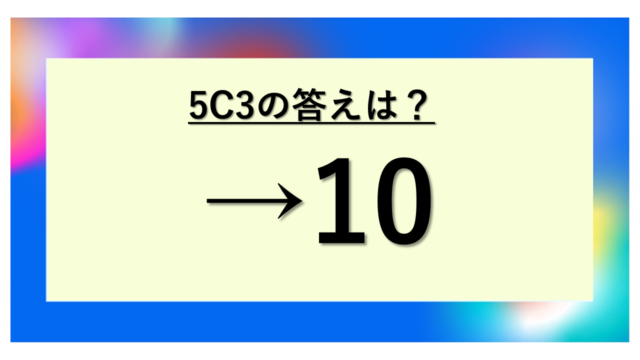
4C2の計算結果は6通り

4C2の答えは6となります。

これは4個のものから2個を選ぶ組み合わせが、全部で6通り存在することを意味しているのです。具体的にA、B、C、Dという4つの要素があった場合、2つを選ぶ組み合わせは以下の6通りになります。

このように実際に書き出してみると、確かに6通りあることが確認できますね。

組み合わせでは順序を考慮しないため、(A, B)と(B, A)は同じものとして扱われます。この点が順列との大きな違いでしょう。

組み合わせnCrの基本的な意味

nCrという表記は「Combination(組み合わせ)」を表す数学記号です。

nは全体の個数、rは選ぶ個数を意味しており、「n個の中からr個を選ぶ組み合わせの総数」を計算できます。4C2の場合、n=4、r=2ということになりますね。

組み合わせの特徴として重要なのは、選んだ要素の順序は関係ないという点です。例えば、クラスから委員を2名選ぶ場合、AさんとBさんを選ぶのと、BさんとAさんを選ぶのは同じ結果になります。

一方、順列(nPr)では順序が重要になるため、計算結果も異なってくるのです。この違いをしっかり理解することが、場合の数の問題を解く上での基礎となるでしょう。

4C2が使われる実際の場面

4C2の計算は、日常生活の様々な場面で活用されています。

例えば、4人でダブルステニスをする際のペアの組み合わせを考える場面です。A、B、C、Dの4人がいた場合、どの2人をペアにするかという選択肢は6通り存在します。

場面	具体例	組み合わせ数
スポーツ	4人から2人のペアを作る	6通り
食事	4種類のメニューから2品選ぶ	6通り
会議	4名の候補から2名の委員を選出	6通り
旅行	4つの観光地から2箇所を訪問	6通り

また、カフェで4種類のトッピングから2つを選ぶ場合や、4冊の本から2冊を選んで読む場合なども同様です。

このように組み合わせの考え方は、選択や分類が必要な様々な状況で役立ちます。数学の問題としてだけでなく、実生活での意思決定にも応用できる重要な概念なのです。

4C2の計算方法を公式で求める手順

続いては、4C2を公式を用いて計算する方法を確認していきます。

組み合わせの公式nCr=n!/(r!(n-r)!)

組み合わせを計算する基本公式は以下の通りです。

この公式に4C2を当てはめると、n=4、r=2となります。

階乗(!)という記号は、その数から1ずつ減らしながら1まで掛け算していく操作を表しているのです。例えば、4!=4×3×2×1=24となります。

公式を理解することで、どんな組み合わせの問題にも対応できるようになるでしょう。特に大きな数の組み合わせを計算する際には、この公式が非常に有効です。

ただし、階乗の計算は数が大きくなると複雑になるため、約分できる部分を見つけることがポイントになります。

4C2を公式に代入して計算する

それでは実際に4C2を公式に代入して計算してみましょう。

このように段階的に計算していくと、答えが6になることが分かります。

ただし、毎回このように全ての階乗を展開する必要はありません。実は、約分を先に行うことで計算をもっと簡単にできるのです。

例えば、4!=4×3×2×1ですが、分母に2!=2×1があるため、この部分は約分できます。すると4C2=(4×3)/(2×1)=12/2=6という、より簡潔な計算になるでしょう。

この約分のテクニックを使えば、大きな数の組み合わせでも効率的に計算できます。

簡略化した計算方法と時短テクニック

組み合わせの計算には、さらに効率的な方法があります。

一般的に、nCrを計算する際は以下のような簡略式を使うと便利です。

この方法なら、不要な計算を省略できるため時間短縮になります。

また、nCr=nC(n-r)という対称性も覚えておくと便利でしょう。例えば、4C2=4C(4-2)=4C2となり、4C3を計算したい場合は4C1として計算する方が簡単です。

テストや受験では時間が限られているため、こうした計算の工夫が得点に直結します。基本公式を理解した上で、状況に応じて最も効率的な方法を選択できるようになりましょう。

なぜその公式になるのか?4C2の理論的背景

続いては、組み合わせの公式がなぜ成り立つのかという理論的な背景を確認していきます。

順列から組み合わせへの変換の考え方

組み合わせの公式は、実は順列の考え方から導くことができます。

まず、4個から2個を選んで並べる順列4P2を考えてみましょう。順列では順序が重要なので、(A, B)と(B, A)は別々にカウントされます。

しかし、組み合わせでは順序を区別しません。(A, B)と(B, A)は同じ組み合わせとして扱われるのです。

2個を並べる方法は2!=2通りあるため、順列の結果を2!で割れば組み合わせになります。つまり、4C2=4P2/2!=12/2=6となるわけです。

この関係性を一般化すると、nCr=nPr/r!という公式が導けるでしょう。順列と組み合わせの違いを理解することが、公式の本質を掴む鍵になります。

階乗を使う理由と数学的意味

なぜ組み合わせの公式に階乗が登場するのでしょうか。

階乗は「並べ方の総数」を表す数学的な道具です。n個のものを全て並べる方法はn!通りあり、これが順列や組み合わせの計算の基礎となっています。

階乗で割るという操作は、区別しない要素の重複を除外するための数学的な仕組みなのです。

例えば、4C2の場合、4!は4個全ての並べ方、2!は選んだ2個の並べ方、もう一つの2!は選ばなかった2個の並べ方を表しています。これらで割ることで、純粋に「どの2個を選ぶか」だけが残るというわけです。

この理解があれば、公式を丸暗記するのではなく、論理的に導き出せるようになるでしょう。

樹形図や表で理解する組み合わせの本質

視覚的に組み合わせを理解するには、樹形図や表が有効です。

4個(A、B、C、D)から2個を選ぶ過程を樹形図で表現すると、選択の流れが明確に見えてきます。ただし、組み合わせでは順序を考慮しないため、重複を避けるよう注意が必要です。

1個目に選ぶ	2個目に選ぶ(1個目より後ろのみ)	組み合わせ
A	B	(A, B)
	C	(A, C)
	D	(A, D)
B	C	(B, C)
	D	(B, D)
C	D	(C, D)

この表から、体系的に選択していけば重複なく全ての組み合わせを列挙できることが分かります。

また、最初にAを選んだ場合は3通り、Bを選んだ場合は2通り、Cを選んだ場合は1通りとなり、合計3+2+1=6通りという計算もできるでしょう。

このような視覚的・体系的なアプローチは、特に小さな数の組み合わせを確認する際に有効です。公式の結果と実際の列挙が一致することを確認できれば、より深い理解につながります。

4C2の覚え方のコツと関連する組み合わせ

続いては、組み合わせを効率的に覚え、活用するためのコツを確認していきます。

語呂合わせや視覚的イメージで記憶する

組み合わせの公式を覚える際には、視覚的なイメージが効果的です。

「nCrは、n個の中からr個を選ぶChoiceの数」と覚えると、CombinationのCとChoiceのCが結びついて記憶に残りやすくなります。

また、4C2=6という具体例を基準として覚えておくのも有効でしょう。「4人から2人選ぶと6通り」というシンプルなイメージを持っておけば、他の組み合わせを計算する際の感覚が養われます。

さらに、公式を丸暗記するのではなく、「順列を選ぶ個数の階乗で割る」という理屈で理解しておくと、忘れても再構築できます。

数学は暗記科目ではありませんが、基本的な例を覚えておくことで、応用問題にも素早く対応できるようになるでしょう。

4C1、4C3、4C4など関連する計算

4C2を理解したら、他の組み合わせも計算してみましょう。

組み合わせ	計算式	答え	意味
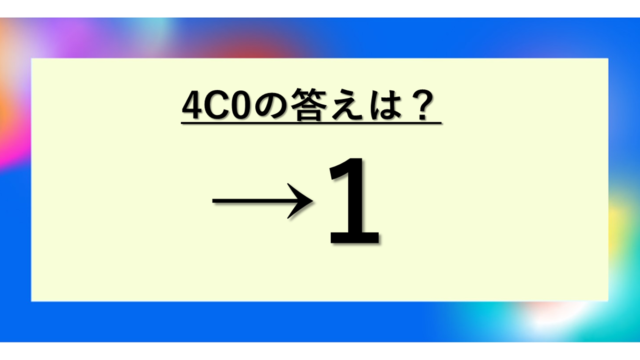
4C0	4! / (0! × 4!) = 1 / 1	1	何も選ばない方法(1通りのみ)
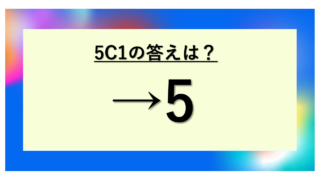
4C1	4! / (1! × 3!) = 4 / 1	4	4個から1個選ぶ
4C2	4! / (2! × 2!) = 24 / 4	6	4個から2個選ぶ
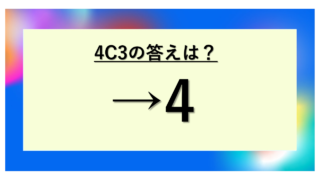
4C3	4! / (3! × 1!) = 24 / 6	4	4個から3個選ぶ
4C4	4! / (4! × 0!) = 1 / 1	1	全て選ぶ方法(1通りのみ)

この表から、4C1=4C3、4C0=4C4という対称性が確認できます。

これはnCr=nC(n-r)という性質の具体例であり、計算の効率化に役立つでしょう。例えば、10C8を計算する際は10C2として計算した方が簡単です。

また、全ての組み合わせを足すと、4C0+4C1+4C2+4C3+4C4=1+4+6+4+1=16=2^4となります。これは「各要素を選ぶか選ばないかの2択がn個あるため、全体で2^n通り」という別の視点からの説明になるのです。

こうした関連性を理解することで、組み合わせの全体像が見えてくるでしょう。

確率問題への応用例と練習問題

組み合わせは確率計算で頻繁に使用されます。

例えば、4枚のカード(A、B、C、D)から2枚を引く試行を考えてみましょう。全ての組み合わせは4C2=6通りです。

このように、組み合わせの総数を分母、条件を満たす組み合わせの数を分子とすることで確率が計算できます。

より複雑な例として、「4枚から2枚引いたとき、少なくとも1枚がAまたはBである確率」を考えてみましょう。この場合、余事象(AもBも含まれない)を使うと効率的です。

AもBも含まれない組み合わせは、残りのCとDから2枚選ぶので2C2=1通り。したがって、求める確率は1-1/6=5/6となります。

このように組み合わせは、単なる計算技術ではなく、実際の確率問題を解く強力なツールなのです。練習問題を通じて、様々なパターンに慣れていきましょう。

まとめ

4C2の計算方法と答えについて詳しく解説してきました。

4C2は「4個から2個を選ぶ組み合わせの数」で、答えは6です。公式nCr=n!/(r!(n-r)!)に代入すると、4C2=4!/(2!×2!)=24/4=6と計算できます。

組み合わせは順序を考慮しない選び方の総数を表しており、日常生活の様々な場面で活用されています。ペア作りやメニュー選択など、身近な問題にも応用できる重要な概念でしょう。

公式を理解する際には、順列との関係性や階乗の意味を把握することが大切です。順列を選んだ個数の階乗で割ることで組み合わせが求められるという原理を理解すれば、公式を忘れても再構築できます。

また、nCr=nC(n-r)という対称性や、簡略化した計算方法を活用することで、効率的に問題を解けるようになります。視覚的なイメージや具体例を通じて理解を深め、確率問題への応用力も養っていきましょう。

組み合わせの計算は、数学の様々な分野の基礎となる重要なスキルです。4C2という基本的な例をしっかり理解することで、より複雑な問題にも自信を持って取り組めるようになるでしょう。