4C1の計算方法や答えは(数学の確率・場合の数・組み合わせ)? 求め方や覚え方のコツも!4C3と同じ?【なぜ】

数学の確率や場合の数を学習していると、必ず登場するのが「組み合わせ」の計算です。中でも4C1という記号は、基礎的でありながら重要な概念を含んでいます。

この記号を見て「どうやって計算するの?」「なぜこの答えになるの?」と疑問に思った経験はありませんか。また、4C1と4C3の答えが同じになることに気づいて、不思議に感じた方もいるでしょう。

組み合わせの計算は、一見複雑に見えますが、その本質を理解すれば驚くほどシンプルです。公式を丸暗記するだけでなく、なぜその答えになるのかという理由まで理解することで、応用問題にも対応できる力が身につきます。

この記事では、4C1の計算方法を基礎から丁寧に解説し、求め方のコツや覚え方、さらには4C3との意外な関係性まで、わかりやすくお伝えしていきます。数学が苦手な方でも理解できるよう、具体例を交えながら説明していきますので、ぜひ最後までお読みください。

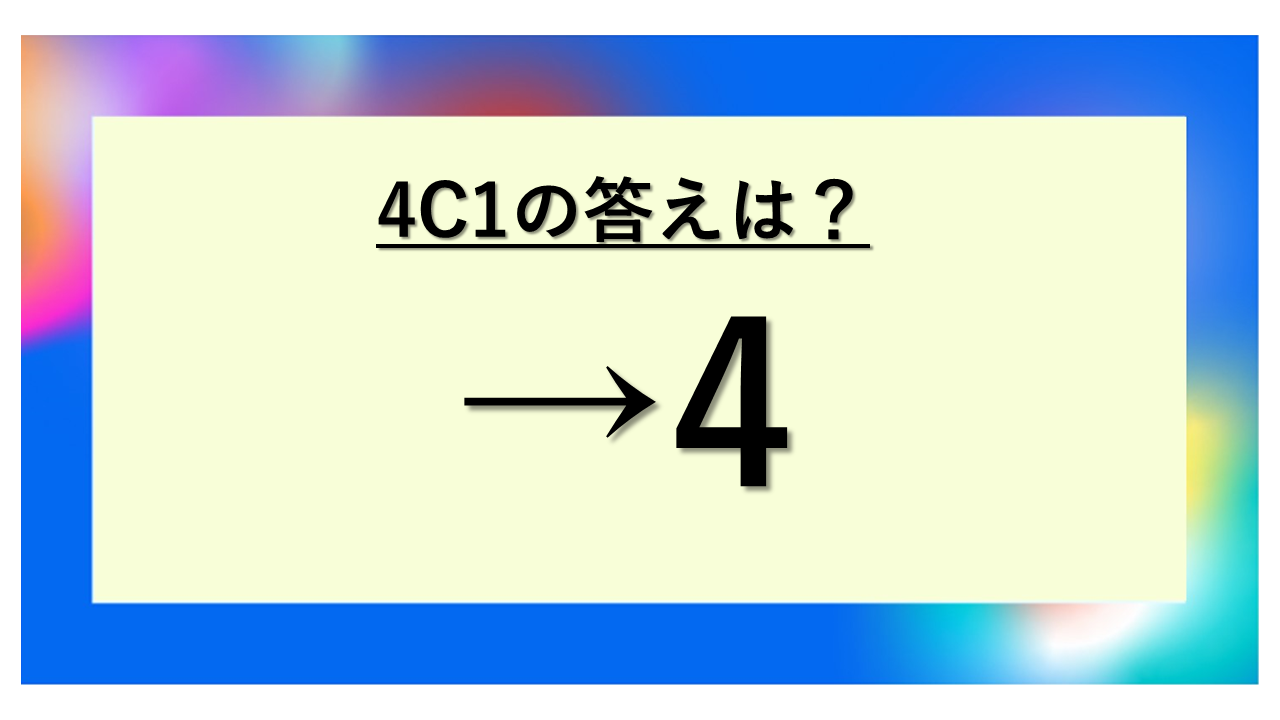
4C1の答えは4!計算方法と求め方の基本

それではまず、4C1の基本的な計算方法について解説していきます。

4C1とは何を表す記号なのか

4C1という記号は、「4個のものから1個を選ぶ組み合わせの総数」を表しています。

「C」はCombination(組み合わせ)の頭文字で、左側の数字が「全体の個数」、右側の数字が「選ぶ個数」を意味します。つまり4C1は、4つの選択肢の中から1つだけを選ぶ方法が何通りあるかを求める計算です。

例えば、A、B、C、Dという4人の中から1人を選ぶ場合を考えてみましょう。選べる人はA、B、C、Dの4通りですよね。これが4C1の答えになります。

組み合わせでは、選ぶ順序は関係ありません。「AとBを選ぶ」と「BとAを選ぶ」は同じ組み合わせとして扱われるのです。

4C1の計算公式と実際の求め方

4C1を公式を使って計算してみましょう。組み合わせの一般的な公式は次の通りです。

階乗記号「!」は、その数から1ずつ減らしながらすべて掛け合わせることを意味します。4! = 4 × 3 × 2 × 1 = 24という計算になります。

実は、4C1のように「n個からr個を選ぶ」場合でr=1のときは、常にnと同じ答えになります。なぜなら、n個の中から1個だけ選ぶ方法はn通りしかないからです。

したがって、4C1 = 4という答えが導かれます。計算を省略しても、直感的に答えがわかる便利なケースですね。

具体例で理解する4C1の意味

実際の場面で4C1がどのように使われるか、いくつか例を見ていきましょう。

どの例でも、4つの選択肢から1つを選ぶパターンは必ず4通りになることがわかります。

日常生活でも、メニューから1品を選ぶ、曜日を1日選ぶなど、組み合わせの考え方は頻繁に使われています。4C1は組み合わせの最も基本的な形であり、この理解が他の複雑な計算の土台となるのです。

4C1と4C3が同じ答えになる理由【なぜ】

続いては、4C1と4C3の興味深い関係性を確認していきます。

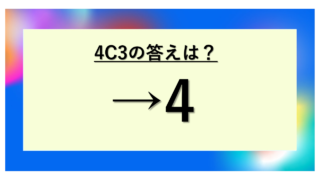
4C3を実際に計算してみる

まず、4C3を公式に当てはめて計算してみましょう。

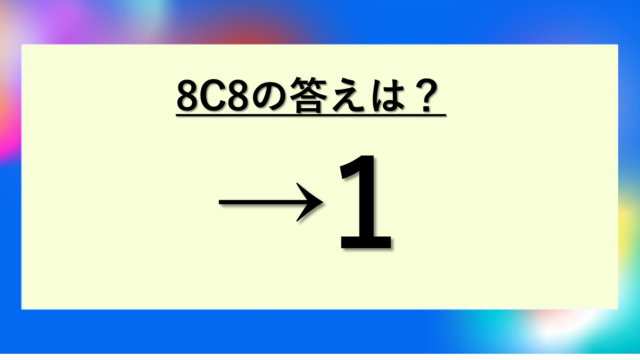
計算の結果、4C3 = 4となりました。これは4C1と全く同じ答えです。

4C3は「4個のものから3個を選ぶ組み合わせ」を表しています。具体的には、A、B、C、Dという4つから3つを選ぶ方法です。

実際に書き出すと、{A,B,C}、{A,B,D}、{A,C,D}、{B,C,D}の4通りになります。確かに計算結果と一致していますね。

選ぶことと残すことの対称性

なぜ4C1と4C3が同じ答えになるのでしょうか。その理由は「選ぶ」と「残す」の対称性にあります。

4つから1つを選ぶということは、裏を返せば3つを残すということです。逆に、4つから3つを選ぶということは、1つを残すということになります。

選ぶ個数	残す個数	組み合わせ数
1個	3個	4通り
3個	1個	4通り

A、B、C、Dから1つ選ぶ(4C1)パターンと、3つ選ぶ(4C3)パターンは、実は表裏一体の関係なのです。

Aを選ぶ → B、C、Dを残す
B、C、Dを選ぶ → Aを残す

このように、選ぶ対象と残す対象が完全に対応しているため、組み合わせの数が同じになります。

一般化した公式nCr = nC(n-r)

この関係は4C1と4C3に限った話ではありません。一般的に次の公式が成り立ちます。

この公式を使えば、計算を簡略化できる場面が多くあります。例えば、100C98を計算する場合、直接計算するよりも100C2として計算する方がはるかに簡単です。

この対称性を理解しておくと、計算ミスを減らし、効率的に問題を解くことができるでしょう。組み合わせの本質を捉えた重要な性質なのです。

組み合わせ計算の覚え方とコツ

続いては、組み合わせ計算をマスターするための実践的なコツを確認していきます。

階乗の計算を素早く行う方法

組み合わせの計算では階乗を扱いますが、実はすべての階乗を計算する必要はありません。

例えば、6C2を計算する場合を見てみましょう。

このように、共通部分を約分してから計算すると、大きな数の掛け算を避けられます。

一般的に、nCrを計算するときは次のように簡略化できます。

– 分子: nから連続してr個の数を掛ける
– 分母: r!を計算する
– 約分しながら計算する

この方法を使えば、電卓なしでも暗算できる問題が増えるでしょう。

小さい方の数に注目する計算テクニック

nCrの公式では、rと(n-r)のどちらか小さい方を使うと計算が楽になります。

元の式	変換後	理由
10C8	10C2	2 < 8 なので計算が簡単
50C48	50C2	2 < 48 なので大幅に簡略化
7C3	7C4	どちらでも可(ほぼ同じ労力)

特に、選ぶ個数が全体の半分を超える場合は、必ず補数を使った方が効率的です。

試験では時間制限がありますから、このテクニックを使って計算時間を短縮しましょう。正確さとスピードの両方が求められる場面で威力を発揮します。

パターン認識で素早く答えを出す

頻出パターンを覚えておくと、瞬時に答えが出せるケースがあります。

また、パスカルの三角形を知っていると、小さな数の組み合わせは暗記不要で導けます。

“`
1
1 1
1 2 1
1 3 3 1
1 4 6 4 1
1 5 10 10 5 1
“`

この三角形の各行がnC0、nC1、nC2…を表しています。4段目を見ると、4C0=1、4C1=4、4C2=6、4C3=4、4C4=1となっていますね。

規則性を理解すれば、計算ミスを防ぎ、答えの妥当性を素早くチェックできるようになるでしょう。

場合の数と確率での活用場面

続いては、実際の問題で組み合わせがどのように使われるかを確認していきます。

確率問題での組み合わせの使い方

確率の問題では、「全体の場合の数」と「条件を満たす場合の数」を求める際に組み合わせが活躍します。

このように、組み合わせを使って場合の数を正確に数えることが確率計算の基本となります。

特に、「少なくとも」「ちょうど」「最大」といった条件がついた問題では、組み合わせの計算が不可欠です。

順列(P)と組み合わせ(C)の使い分けも重要なポイントでしょう。順序が関係あるときは順列、順序が関係ないときは組み合わせを使います。

実生活での組み合わせの応用例

組み合わせの考え方は、数学の問題だけでなく実生活でも幅広く応用されています。

場面	組み合わせの例	計算式
チーム編成	10人から5人のチームを作る	10C5 = 252通り
メニュー選択	8種類から3品を選ぶ	8C3 = 56通り
宝くじ	43個から6個の数字を選ぶ	43C6 = 6,096,454通り

ビジネスシーンでは、プロジェクトメンバーの選定や商品の組み合わせパターンの計算などに活用されます。

また、統計学やデータ分析の分野でも、サンプリング方法や実験計画を立てる際に組み合わせの知識が必要です。

数学の授業で学ぶ組み合わせは、実は私たちの身の回りで日常的に使われている概念なのです。

よくある間違いと注意点

組み合わせの計算でよくある間違いを確認しておきましょう。

特に注意が必要なのは、「並べる」のか「選ぶだけ」なのかの区別です。

問題文に「順番に」「1位から」などの表現があれば順列、「グループを作る」「選ぶ」だけなら組み合わせと判断します。

また、同じものを含む組み合わせ(重複組み合わせ)は別の公式を使うため、問題の条件をよく読むことが大切でしょう。

計算の途中で約分できる部分を見逃さないことも、正確で効率的な計算のポイントです。ミスを減らすには、答えが妥当な範囲に収まっているか確認する習慣をつけると良いでしょう。

まとめ

4C1の計算方法と組み合わせの基本について解説してきました。

4C1は「4個から1個を選ぶ組み合わせ」を表し、答えは4となります。公式を使った計算だけでなく、なぜその答えになるのかという本質を理解することが重要です。

特に注目すべきは、4C1と4C3が同じ答えになるという性質でしょう。これは「選ぶ」と「残す」が表裏一体の関係にあることを示しており、nCr = nC(n-r)という一般公式として応用できます。

組み合わせの計算をマスターするコツは、階乗の約分を活用すること、小さい方の数に注目すること、頻出パターンを覚えることです。これらのテクニックを使えば、複雑な計算も素早く正確に解けるようになります。

場合の数や確率の問題では、組み合わせが基礎となる重要な概念です。順列との使い分けに注意しながら、実際の問題で応用していきましょう。

数学の公式は丸暗記するだけでなく、その意味や成り立ちを理解することで、応用力が大きく向上します。4C1という基本的な計算から始めて、組み合わせ全体の理解を深めていってください。