数学の組み合わせの問題を解いていると、「2C0」という表記に出会うことがあるでしょう。
この記号を見て「ゼロ個選ぶってどういうこと?」「答えは0じゃないの?」と疑問に思った方も多いのではないでしょうか。
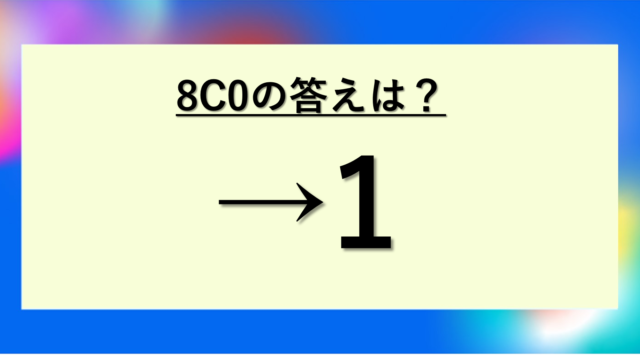
実は2C0の答えは1になります。一見不思議に感じるこの結果には、数学的にしっかりとした理由があるのです。
今回の記事では、2C0の計算方法や答えだけでなく、なぜそうなるのかという理由、さらには覚え方のコツまで詳しく解説していきます。
組み合わせの基本をマスターして、確率や場合の数の問題をスムーズに解けるようになりましょう。
2C0の計算方法と答えについて
それではまず、2C0の計算方法と答えについて解説していきます。
2C0の答えは1
結論から言うと、2C0=1です。
この答えに「え、ゼロ個選ぶのに1になるの?」と驚く方もいるかもしれません。しかし、組み合わせの定義と計算式に従えば、この答えは自然に導かれるのです。
nCrの組み合わせの公式は次のように表されます。
ここで、n!は「nの階乗」を意味し、n! = n × (n-1) × (n-2) × … × 2 × 1
この公式に n=2、r=0 を代入してみましょう。
2C0の計算過程
2C0を公式に当てはめて計算していきます。
= 2! / (0! × 2!)
= 2! / (0! × 2!)
ここで重要なのが0!の値です。
階乗の定義では、0! = 1 と定められています。これは約束事として覚えておく必要があるでしょう。
したがって計算を続けると次のようになります。
= 2! / 2!
= 1
このように、2C0の計算結果は1となるわけです。

nC0が常に1になる理由
続いては、なぜnC0が常に1になるのかという理由を確認していきます。
数学的な理由
実は2C0だけでなく、どんな自然数nに対してもnC0=1が成り立ちます。
これを一般的な公式で確認してみましょう。
= n! / (1 × n!)
= n! / n!
= 1
0! = 1 という定義があるため、どんなnの値でも計算結果は必ず1になるのです。
これは数学の美しい性質の一つと言えるでしょう。
直感的な理解方法
「ゼロ個選ぶのに1通り?」という疑問を解消するには、「何も選ばない」という選び方も1つの選び方だと考えると分かりやすいでしょう。
例えば、2つのボール(赤と青)があるとします。この中から0個選ぶ方法は何通りあるでしょうか。
「赤を選ばず、青も選ばない」という選び方が唯一の方法なのです。
つまり、何も選ばないという状態自体が1つの確定した状態であり、それ以外の「何も選ばない方法」は存在しないということ。
この考え方を理解すると、nC0=1という結果に納得できるのではないでしょうか。
組み合わせnCrの基本と計算方法
続いては、組み合わせnCrの基本と計算方法について確認していきます。
組み合わせとは何か
組み合わせ(Combination)とは、n個のものからr個を選ぶときの選び方の総数を求める計算方法です。
重要なのは、組み合わせでは順序を考えないという点でしょう。
例えば、A、B、Cという3人から2人を選ぶとき、「AとB」と「BとA」は同じ組み合わせとして数えます。これが順列との大きな違いです。
nCrの計算公式
組み合わせの計算には、以下の公式を使用します。
または
nCr = (n × (n-1) × (n-2) × … × (n-r+1)) / r!
下の公式は、階乗の計算を簡略化したものです。
大きな数字を扱うときには、こちらの方が計算しやすいこともあるでしょう。
具体例で理解を深める
いくつかの具体例を見てみましょう。
3C2 = 3! / (2! × 1!)
= (3 × 2 × 1) / (2 × 1 × 1)
= 6 / 2
= 3
3つのものから2つを選ぶ方法は3通り
5C3 = 5! / (3! × 2!)
= (5 × 4 × 3 × 2 × 1) / (3 × 2 × 1 × 2 × 1)
= 120 / 12
= 10
5つのものから3つを選ぶ方法は10通り
このように、公式に当てはめて計算すれば、どんな組み合わせの数も求められます。
組み合わせの重要な性質
続いては、組み合わせの重要な性質を確認していきます。
nCr = nC(n-r)の対称性
組み合わせには、nCr = nC(n-r)という美しい性質があります。
これは「n個からr個を選ぶ」ことと「n個からr個を選ばない(つまりn-r個を選ぶ)」ことが同じ数になるという意味です。
5C2 = 5! / (2! × 3!) = 120 / 12 = 10
5C3 = 5! / (3! × 2!) = 120 / 12 = 10
確かに両方とも10になる
この性質を利用すると、計算を簡単にできることもあるでしょう。
例えば、100C98を計算したいとき、100C2として計算する方が圧倒的に楽になります。
nCnとnC1の特別な値
組み合わせには、覚えておくと便利な特別な値がいくつかあります。
| 組み合わせ | 計算式 | 結果 | 意味 |
|---|---|---|---|
| nC0 | n! / (0! × n!) | 1 | 何も選ばない方法は1通り |
| nC1 | n! / (1! × (n-1)!) | n | 1つだけ選ぶ方法はn通り |
| nCn | n! / (n! × 0!) | 1 | 全部選ぶ方法は1通り |
| nC(n-1) | n! / ((n-1)! × 1!) | n | 1つだけ残す方法はn通り |
これらは「何もしない」「全部選ぶ」という極端な場合ですが、どちらも選び方は1通りしかないのです。
2C0を含む組み合わせの計算例
続いては、2C0を含む実際の計算例を確認していきます。
2Crの全パターン
2つのものから選ぶ組み合わせには、以下のパターンがあります。
2C0 = 2! / (0! × 2!) = 2 / 2 = 1
2C1の計算
2C1 = 2! / (1! × 1!) = 2 / 1 = 2
2C2の計算
2C2 = 2! / (2! × 0!) = 2 / 2 = 1
これを表にまとめると分かりやすいでしょう。
| 選ぶ個数 | 組み合わせの記号 | 計算結果 | 具体例(A、Bから選ぶ場合) |
|---|---|---|---|
| 0個 | 2C0 | 1 | { }(何も選ばない) |
| 1個 | 2C1 | 2 | {A}、{B} |
| 2個 | 2C2 | 1 | {A, B} |
合計すると1+2+1=4通りです。これは2の2乗に等しく、すべての部分集合の個数と一致します。
二項定理との関係
実は組み合わせの総和には、美しい規則性があります。
これを二項定理と呼びます。
2の場合で確認してみましょう。
確かに成り立っている
この関係を理解すると、組み合わせの計算ミスを発見しやすくなるでしょう。
0!が1である理由
続いては、なぜ0!が1と定義されるのかという理由を確認していきます。
階乗の連続性から考える
階乗には次のような性質があります。
この式を変形すると、(n-1)! = n! / n となりますね。
この関係をn=1の場合に適用してみましょう。
このように、階乗の定義を自然に拡張すると0!=1になるのです。
空積の考え方
もう一つの理解方法として、「空積(からせき)」という概念があります。
何も掛けないときの積は1と定義されるのです。これは足し算において、何も足さないときは0になることに対応しています。
これは数学の体系全体の整合性を保つための重要な定義なのです。
組み合わせの覚え方のコツ
続いては、組み合わせを効率的に覚えるコツを確認していきます。
公式の覚え方
組み合わせの公式は、以下のように段階的に覚えると良いでしょう。
nCr = n! / (r! × (n-r)!)
ステップ2:意味を理解する
分子:n個すべてを並べる方法
分母:選んだr個の順序を消す × 選ばなかったn-r個の順序を消す
ステップ3:簡略形も覚える
nCr = n(n-1)(n-2)…(n-r+1) / r!
公式を丸暗記するのではなく、なぜその形になるのかを理解することが重要です。
特殊な値を暗記する
以下の値は頻出するので、計算せずに答えられるようにしておきましょう。
| パターン | 値 | 覚え方 |
|---|---|---|
| nC0 | 1 | 何も選ばないのは1通り |
| nC1 | n | 1つ選ぶのはn通り |
| nCn | 1 | 全部選ぶのは1通り |
| nC(n-1) | n | 1つ残すのはn通り |
| nCr | nC(n-r) | 選ぶ=残すの対称性 |
これらを覚えておくと、計算時間を大幅に短縮できるでしょう。
計算練習のポイント
組み合わせの計算に慣れるには、以下のような練習が効果的です。
問1:3C0、3C1、3C2、3C3を計算せよ
問2:5C2と5C3を計算し、5C2=5C3が成り立つか確認せよ
問3:4C0+4C1+4C2+4C3+4C4の値を求めよ(ヒント:2^4)
最初は公式を見ながらでも構いません。繰り返し練習することで、自然と身につくでしょう。
まとめ
今回は2C0の計算方法や答え、そしてその理由について詳しく解説してきました。
2C0=1という答えは、一見不思議に感じるかもしれませんが、組み合わせの公式と0!=1という定義から自然に導かれます。
「何も選ばない」という選び方も1つの確定した選び方であるという考え方を理解すると、この結果に納得できるのではないでしょうか。
組み合わせの計算では、nC0=1、nC1=n、nCn=1といった基本的な値を覚えておくこと、そしてnCr=nC(n-r)という対称性を活用することが重要です。
これらの性質を理解し、練習を重ねることで、確率や場合の数の問題をスムーズに解けるようになるでしょう。
数学の美しい規則性を楽しみながら、学習を続けてみてください。